Jeu de Sokoban
Recherche de solutions optimales
Chapitre 1 Remerciements
Je tiens avant tout à remercier Madame Véronique Bruyère d'avoir accepté le sujet de mémoire qui me tenait à cœur et de l'avoir suivi avec enthousiasme tout au long de l'année. Merci pour les nombreux conseils et suggestions qu'elle m'a apportés, entre autres lors de la rédaction.
J'exprime aussi ma reconnaissance à Monsieur Tom Mens pour m'avoir autorisé à utiliser l'un de ses ordinateurs personnels et à Sylvain Degransart pour m'avoir créé un compte sur celui-ci. Les nombreux calculs que j'ai pu y effectuer m'ont permis de progresser plus vite et de détecter mes erreurs plus rapidement.
Je montre également ma gratitude à Monsieur Delgrange et à Monsieur Pirlot pour avoir accepté d'être les rapporteurs de ce mémoire.
Je remercie mes parents pour les nombreuses relectures, souvent difficiles, que je leur ai infligées tout au long de la rédaction de ce mémoire.
Pour finir, je tiens à apporter une reconnaissance toute particulière à mon grand-père maternel, Làszlo Fodor qui, dès ma petite enfance, a su susciter mon intérêt pour de nombreux casse-têtes. Il a été le premier à mettre un Rubik's Cube entre mes mains. Le sujet de ce mémoire ne serait peut-être pas le même sans son influence.
Table des matières
Chapitre 2 Introduction
Un problème de planification est défini par un environnement composé d'objets mouvants et d'obstacles. Dans ce type de problème, nous partons d'une configuration initiale des objets et l'objectif est d'aboutir à une configuration finale en respectant les contraintes du système.
Le jeu de Sokoban, qui représente un cas typique de problème de planification, est un jeu vidéo vieux de près de 30 ans qui est réputé pour ses règles simples et sa relative difficulté. Il possède encore un certain prestige chez les joueurs et dans le milieu scientifique. Dans ce problème, un agent a pour objectif de pousser, à partir d'une configuration initiale, toutes les caisses présentes sur des goals en respectant les règles du jeu. La configuration finale sera donc celle pour laquelle toutes les caisses sont positionnées sur des goals. Le jeu possède plusieurs milliers de niveaux très variés et donc autant de configurations initiales différentes.
Le but de ce mémoire est de réussir à créer un programme permettant de trouver le chemin emprunté par l'agent pour positionner, à partir d'une certaine configuration, toutes les caisses sur les goals.
Le sujet du Sokoban a déjà été abordé dans de nombreuses recherches très poussées. Celles-ci n'avaient pas toutes les mêmes ambitions car certaines essayaient de trouver le plus de solutions possibles alors que d'autres privilégiaient l'obtention de solutions optimales, plus difficiles à trouver et donc moins nombreuses. Les mécanismes intrinsèques qui interviennent diffèrent selon les choix effectués.
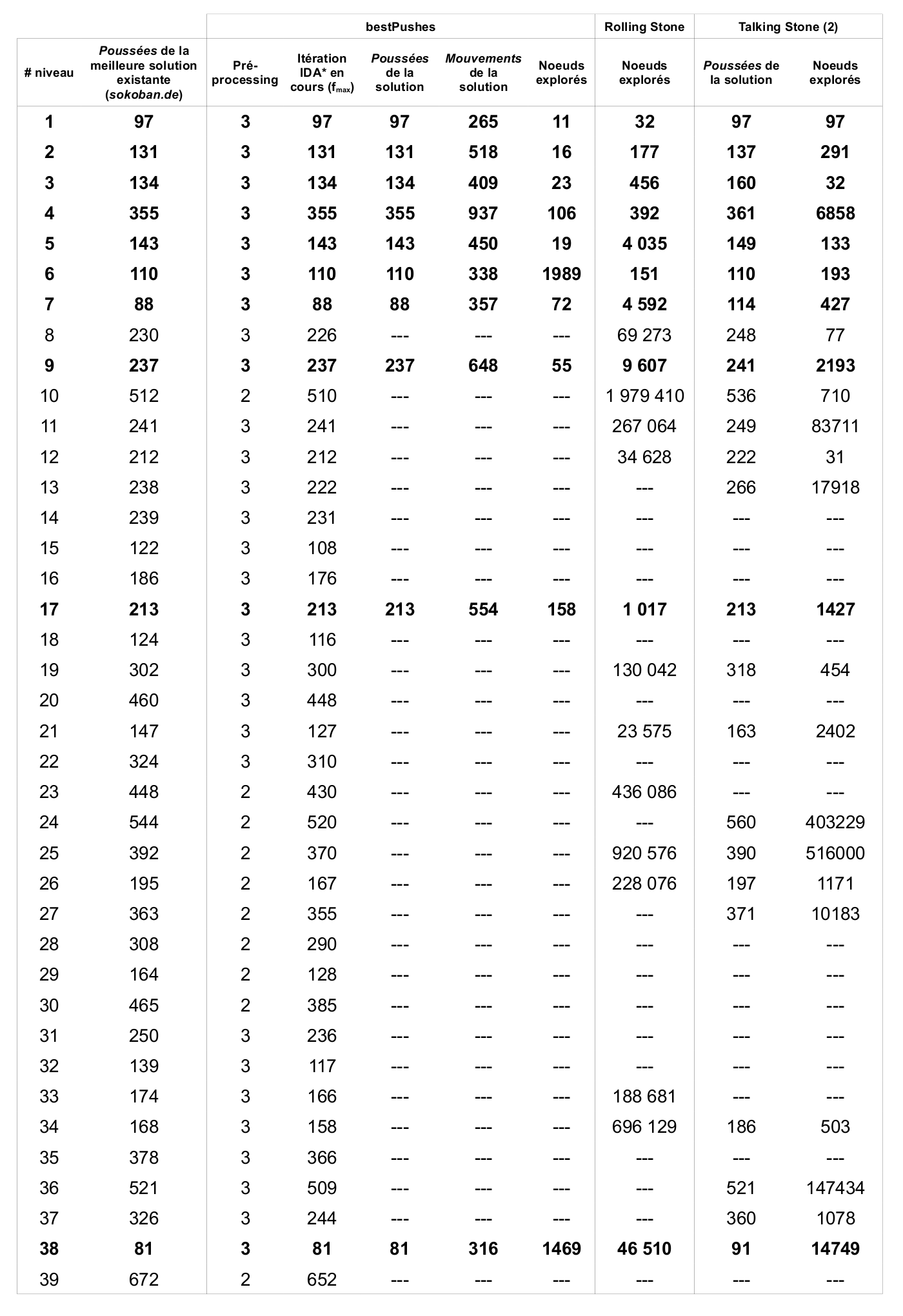
Actuellement, le meilleur programme s'appliquant sur des niveaux de Sokoban s'appelle Sokoban Automatic Solver et permet de résoudre 86 niveaux sur un total de 90 proposés. Les solutions trouvées ne sont cependant pas optimales et les techniques utilisées par le programme ne sont pas du tout documentées. Rolling Stone, un autre programme beaucoup mieux documenté, permet de résoudre 57 niveaux sur 90. Contrairement à Sokoban Automatic Solver, celui-ci trouve des solutions optimales. Ce mémoire va principalement s'inspirer des mécanismes utilisés dans ce programme.
L'objectif de ce mémoire est d'utiliser les techniques existantes pour trouver les solutions optimales des niveaux de Sokoban. Celles-ci seront améliorées quand l'occasion se présentera et certaines nouvelles méthodes, plus ou moins utiles, seront également intégrées.
Le développement de ce sujet se fait en plusieurs grandes parties. La première introduit certaines notions nécessaires pour bien comprendre le fonctionnement du jeu ainsi que les méthodes utilisées pour résoudre les niveaux. Le concept très important d'arbre de recherche y est présenté. Une deuxième grande partie concerne les différents parcours applicables sur l'arbre de recherche. Le parcours IDA*, qui se montre très performant dans notre cas, est détaillé. Les chapitres suivants traitent des estimations, deadlocks et pénalités qui sont trois méthodes permettant de réduire efficacement la taille de l'arbre de recherche. Nous terminons par le pré-traitement et le post-traitement qui permettent de rechercher des résultats intermédiaires qui s'appliqueront sur la prochaine construction de l'arbre de recherche.
Chapitre 3 Le Sokoban
3.1 Historique
Sokoban, gardien d'entrepôt en français, est un jeu vidéo de réflexion originaire du Japon et datant du début des années 80. Selon des sources diversesSoHistory (Pas d'année); WikiSokoban (Pas d'année), il a été créé par Hiroyuki Imabayashi et édité par Thinking Rabbit qui en détient aujourd'hui tous les droits. Le jeu doit sa popularité à des règles très simples mais qui permettent néanmoins une très grande complexité. De fait, certains niveaux sont très difficiles à résoudre par l'homme et même par la machine.
Il possèdait initialement une cinquantaine de niveaux mais une véritable communauté s'est créée et des milliers d'autres sont maintenant disponibles sur Internet. De même, des dizaines d'adaptations ou d'évolutions du jeu existent sur presque tous les supports et avec des graphismes plus ou moins évolués.
Sokoban est un sujet particulièrement intéressant dans les domaines de la complexité et de l'intelligence artificielle. Son facteur de branchement, le nombre de choix possibles pour le joueur à un moment du jeu, est comparable à celui des échecs. Le nombre de décisions à prendre pour réussir à trouver une solution est relativement élevé. Un humain arrive cependant à trouver des heuristiques performantes pour un problème donné, ce qui lui permet d'arriver plus vite à une solution.
3.2 Règles
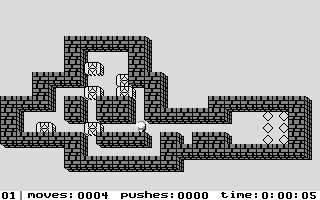
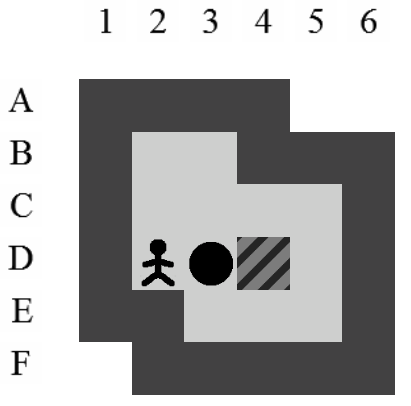
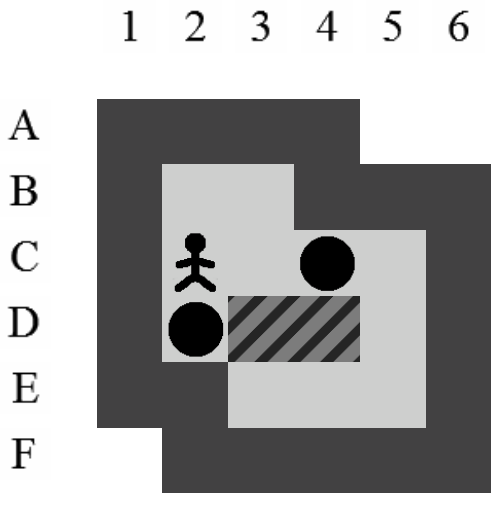
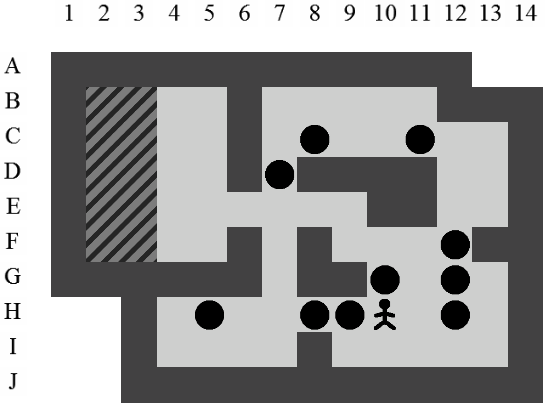
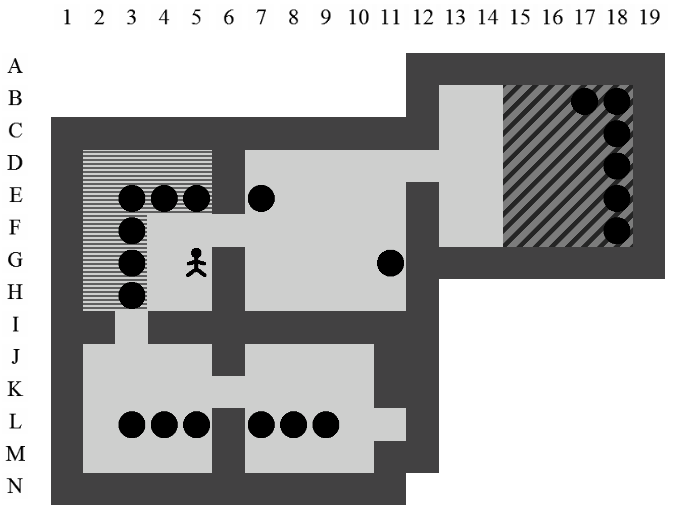
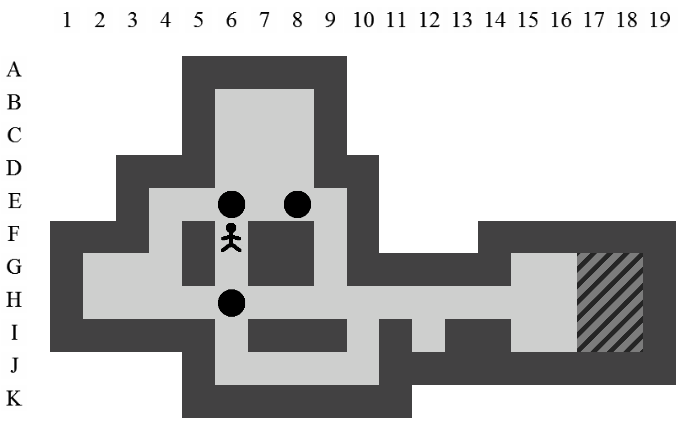
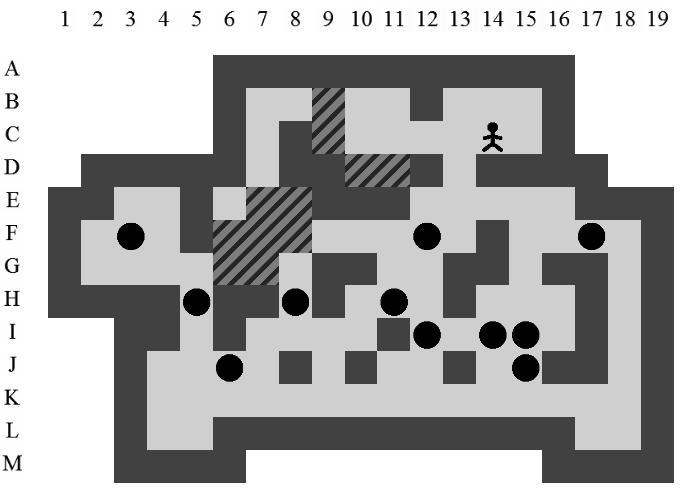
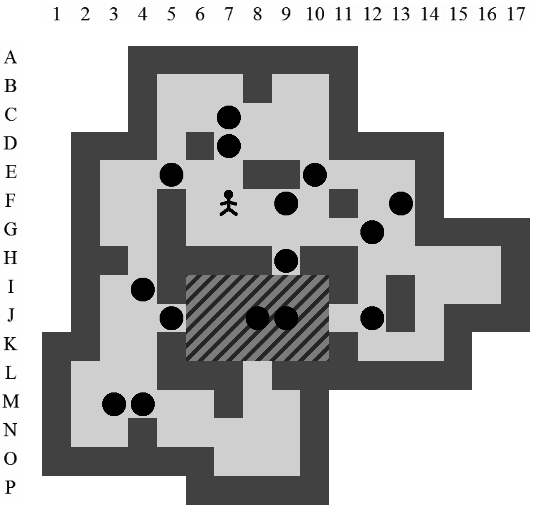
La Figure 3.2 correspond à la représentation d'un niveau de Sokoban.
-
 Un pousseur. Le gardien d'entrepôt.
Un pousseur. Le gardien d'entrepôt. -
 Des murs.
Des murs. -
 Une ou des caisses.
Une ou des caisses. -
 Un ou des goals (au moins autant que de caisses).
Un ou des goals (au moins autant que de caisses). -
 Le sol.
Le sol.
Le joueur dirige le pousseur. Celui-ci peut se déplacer sur les quatre positions qui lui sont directement voisines : haut, bas, gauche et droite. Il peut pousser des caisses mais uniquement une à la fois.
Une poussée se produit si le pousseur se trouve à côté d'une caisse, s'il se dirige dans sa direction et si la position derrière la caisse n'est pas occupée par un mur ni par une autre caisse. Lorsqu'une poussée est effectuée, le pousseur et la caisse se déplacent, en même temps, d'une position.
Si deux caisses voisines sont alignées sur un même axe, le pousseur ne pourra pas les pousser sur cet axe. Les murs délimitent l'aire de jeu. Ni le pousseur ni les caisses ne peuvent les franchir. Le but du jeu est de réussir à positionner toutes les caisses sur des goals. La difficulté réside dans le fait qu'il est impossible pour le pousseur de tirer une caisse.
Si toutes les caisses se situent sur des goals, alors le niveau est réussi et le chemin utilisé par le pousseur est solution du niveau. Il est important de signaler que tous les niveaux doivent posséder au moins une solution.
La solution optimale en terme de mouvements est souvent différente de la solution optimale en terme de poussées. Certains sites Internet comme sokobano.de regroupent les meilleures solutions connues (mouvements et poussées) pour pratiquement tous les niveaux existants.
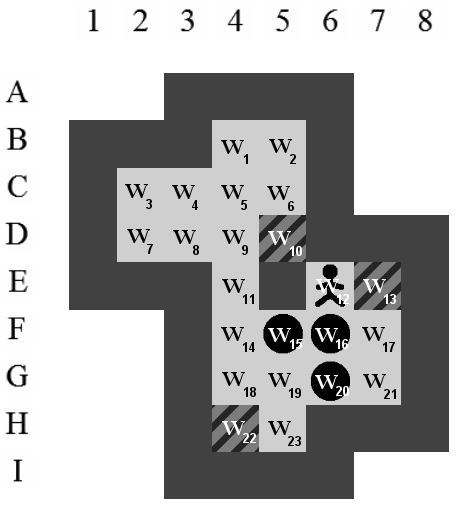
Dans ce document, la référence à l'une des positions de l'aire de jeu se fera toujours à l'aide du croisement entre la ligne et la colonne de la position concernée (i.e. la position du pousseur est I12 sur la Figure 3.2).
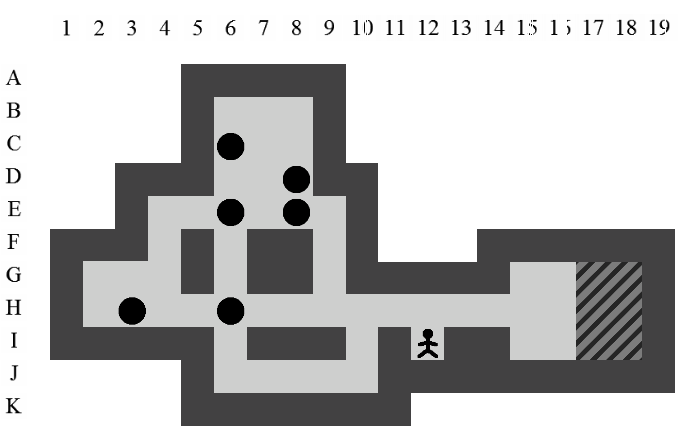
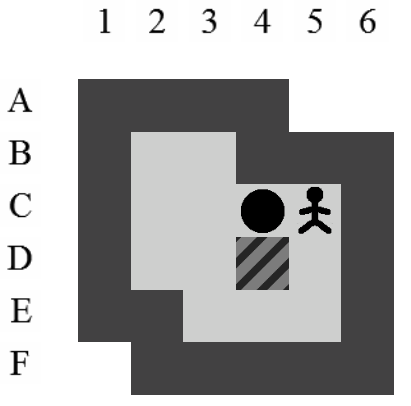
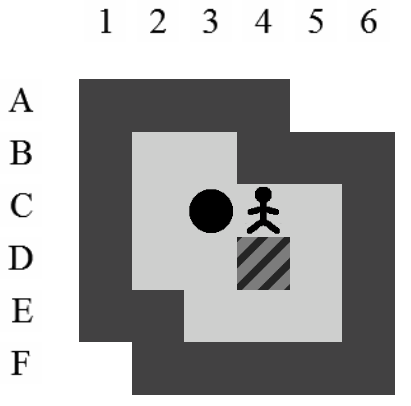
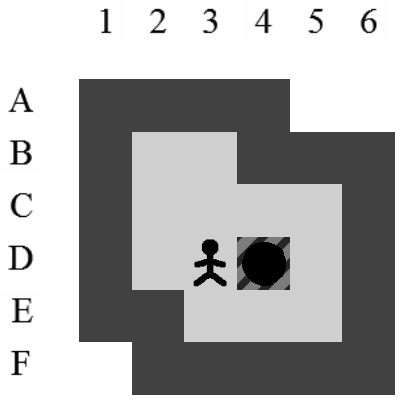
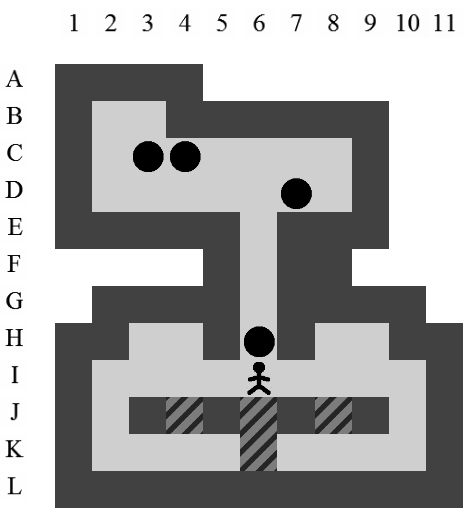
Exemple de solution optimale
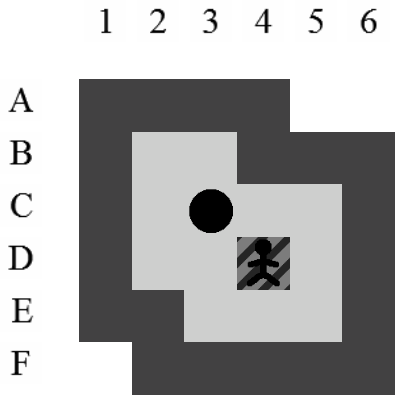
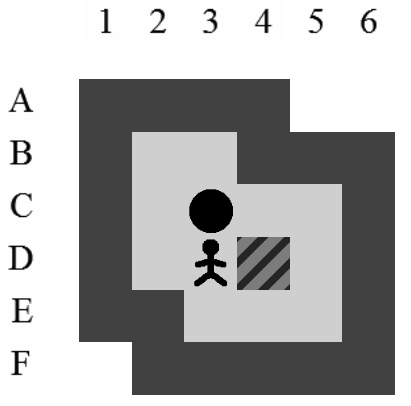
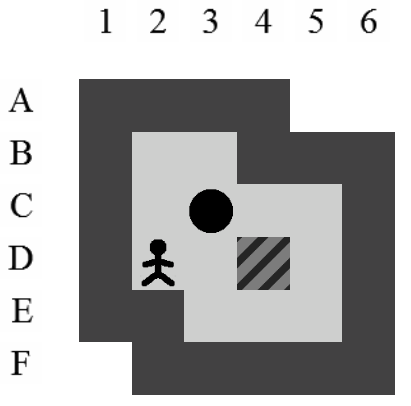
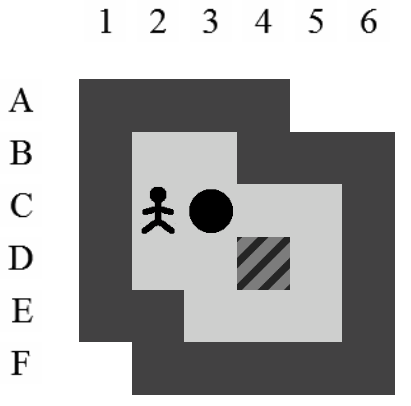
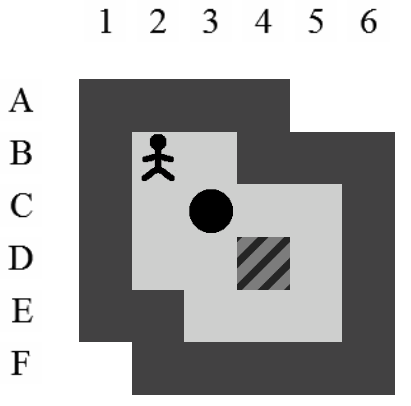
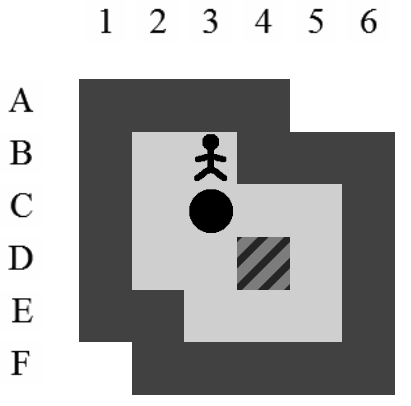
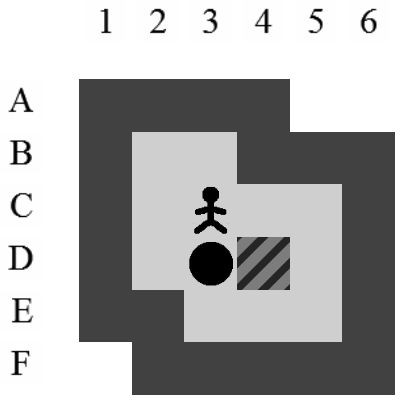
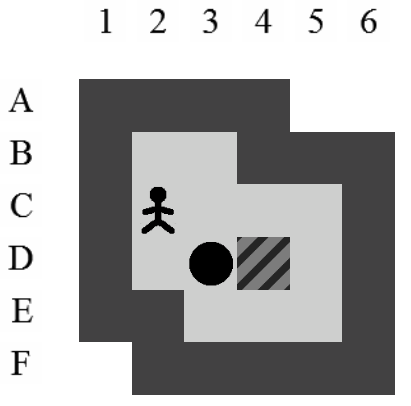
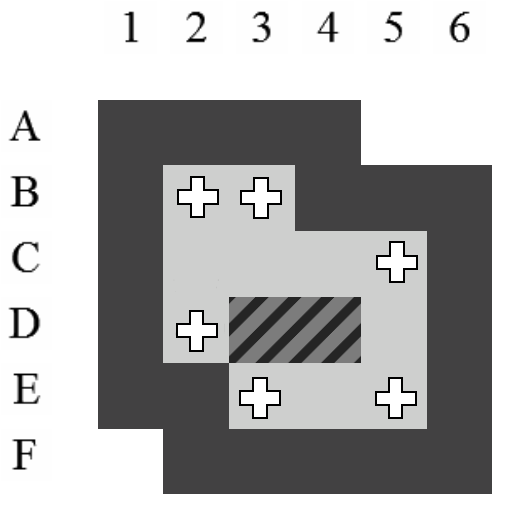
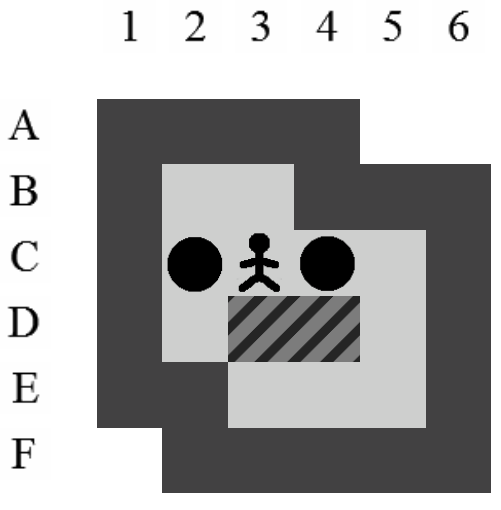
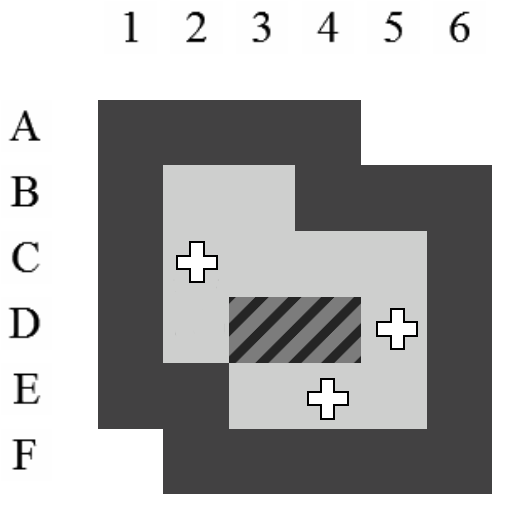
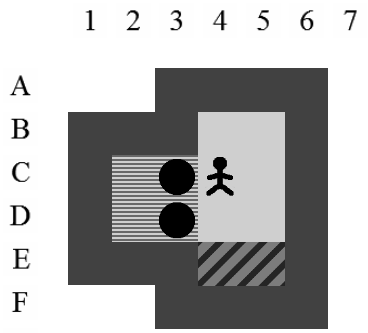
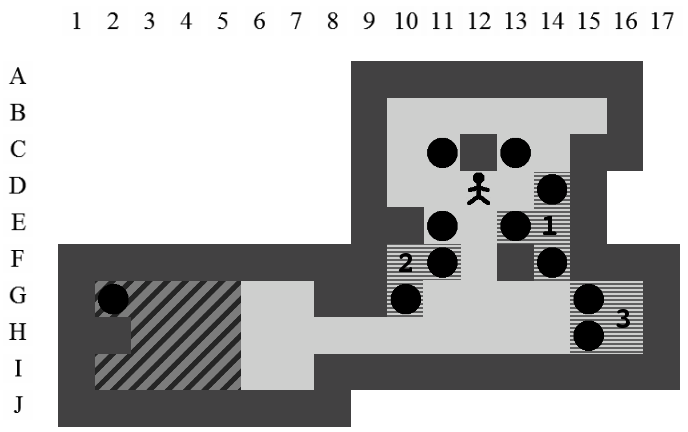
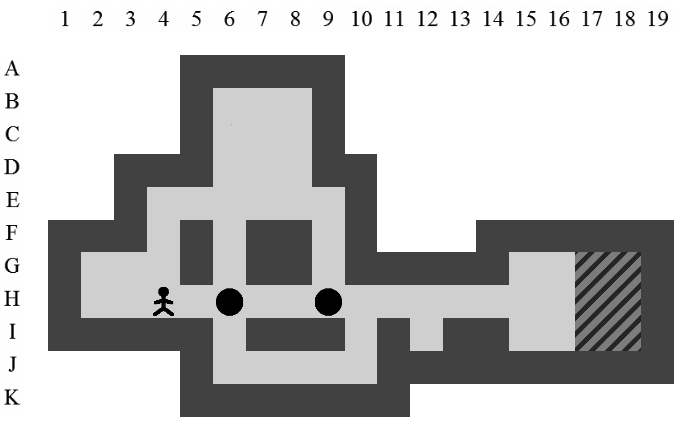
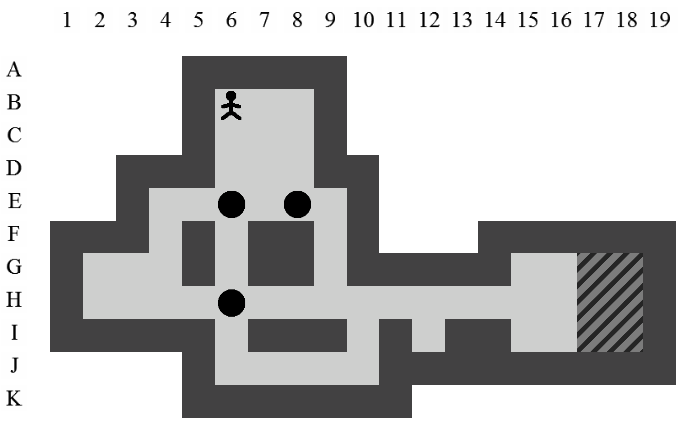
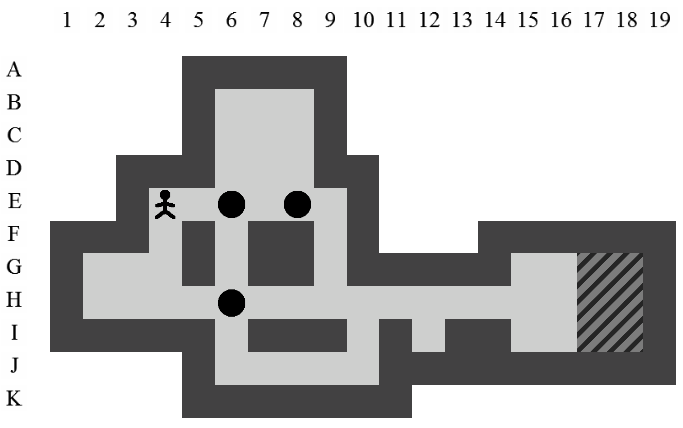
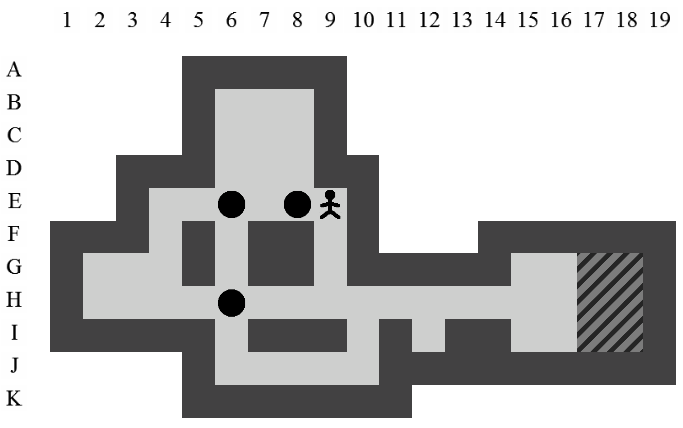
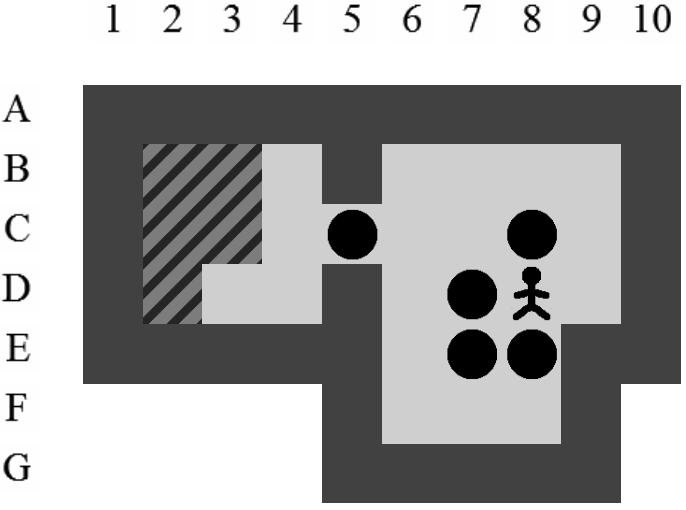
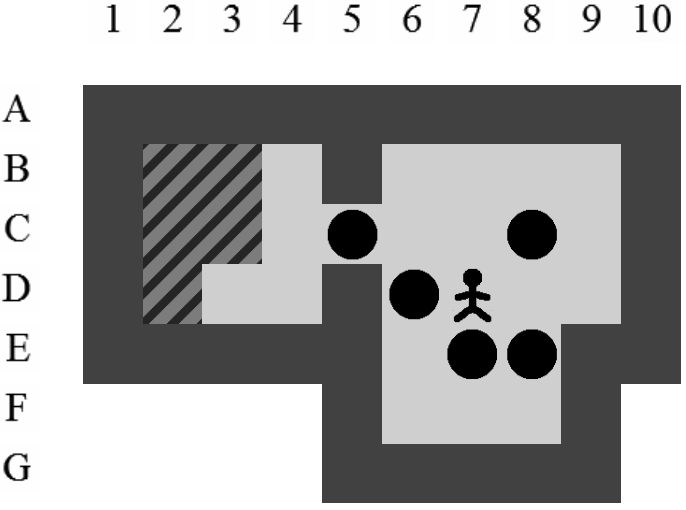
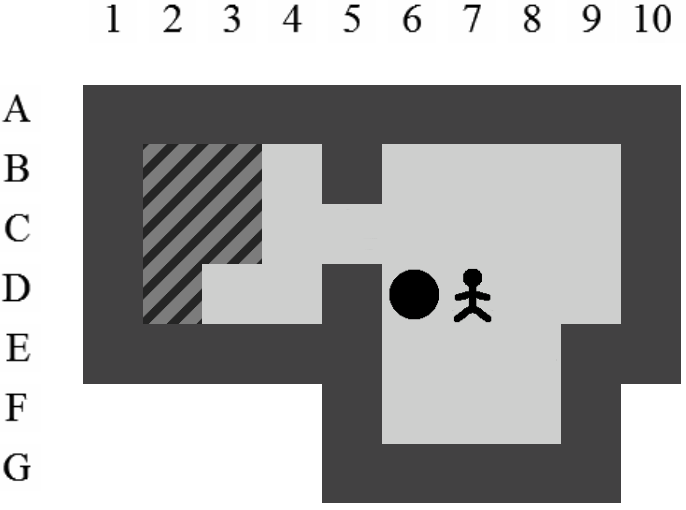
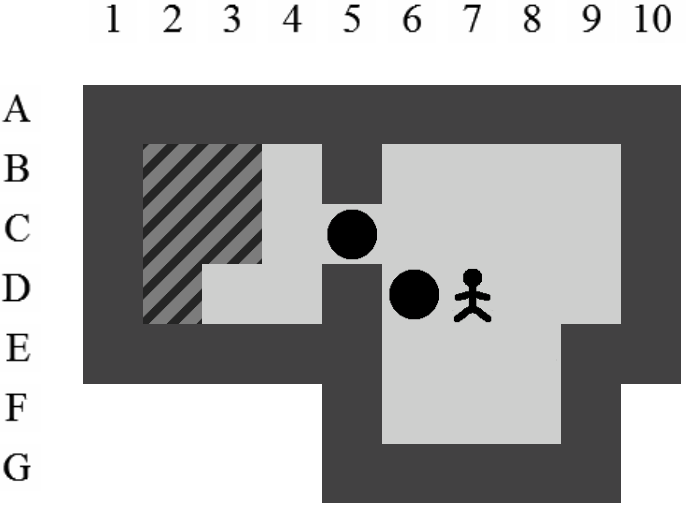
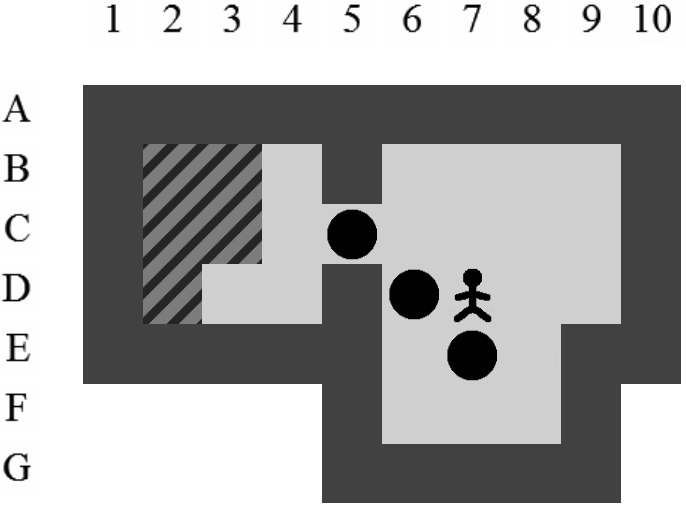
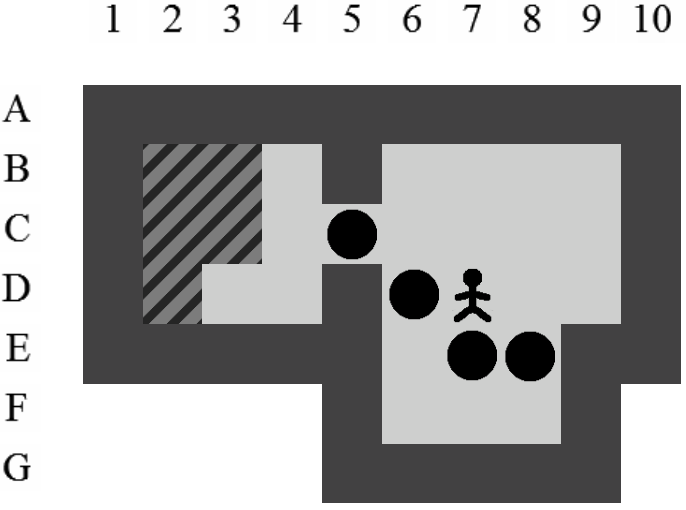
Etant donné le niveau représenté sur la Figure 3.3, la liste des états intermédiaires qui mènent à la solution optimale, en terme de mouvements et de poussées, est visible sur la Figure 3.4. Il y a plusieurs façons de représenter une solution. Celle adoptée dans ce document consiste à se placer du point de vue du pousseur et d'indiquer ses directions successives par des lettres minuscules s'il ne pousse pas de caisse ou majuscules s'il en pousse une. Si plusieurs mouvements ont lieu dans la même direction. La lettre est préfixée par son nombre d'occurences. Dans notre exemple, la solution est Ld2l2urDldR et s'établit en 11 mouvements et 3 poussées.
3.3 Complexité
Il a été démontré en 1995 par Dorit Dor et Uri ZwickDor et Zwick (Pas d'année) que le problème de décision correspondant au Sokoban était NP-difficile. C'est-à-dire que Sokoban fait partie de la classe des problèmes décidables par une machine de Turing non déterministe en temps polynomial.
Deux ans plus tard, en 1997, des travaux réalisés par Joseph CulbersonCulberson (Pas d'année) ont démontré que le problème de décision était PSPACE-complet. Il appartient donc à la classe PSPACE et est PSPACE-difficile. C'est-à-dire qu'il est au moins aussi difficile que tous les problèmes de la classe PSPACE qui représente les problèmes décidables par une machine de Turing déterministe en espace polynomial par rapport à la taille de sa donnée.
Chapitre 4 Résolution
Sokoban est un problème de type Single-Agent. C'est-à-dire qu'un seul agent peut faire évoluer le jeu en permettant le passage d'un état à un autre. Dans le Sokoban, celui-ci est le pousseur. Ce type de problème n'est pas nouveau et des méthodes existent déjà pour transiter d'un état à un autre afin d'atteindre un état solution. Ces méthodes impliquent un arbre de recherche comme nous le verrons dans la Section 4.1.
Les méthodes existantes sont cependant très générales et peu efficaces dans le cas du Sokoban. En effet, elles devront être adaptées aux particularités de ce problème précis sans quoi nous n'obtiendrons que peu de résultats. La Section 4.2 détaille comment des études menées par différentes Universités ont déjà grandement amélioré les méthodes existantes.
Les méthodes Single-Agent et certaines des améliorations propres au Sokoban seront intégrées dans ce mémoire. Devant la quantité de techniques qui existent, un choix a dû être effectué pour sélectionner celles qui semblaient les plus prometteuses. De plus, certaines évolutions et alternatives seront proposées. Les décisions prises quant à ces techniques sont détaillées dans la Section 4.3.
4.1 Arbre de recherche
Comme expliqué précédemment, la méthode de base pour résoudre un problème de Sokoban est la même que pour la plupart des problèmes de type Single-Agent. Il convient de commencer par définir un état initial. Cet état initial reprend la position du pousseur et celles des caisses dans le niveau. À partir de cet état et en respectant les règles du jeu, nous regardons toutes les transitions possibles vers de nouveaux états. Cette procédure est répétée récursivement pour tous les états et un arbre de recherche est ainsi construit. Lorsqu'un état est solution, il suffit de remonter dans l'arbre pour trouver le chemin menant de la racine à la solution.
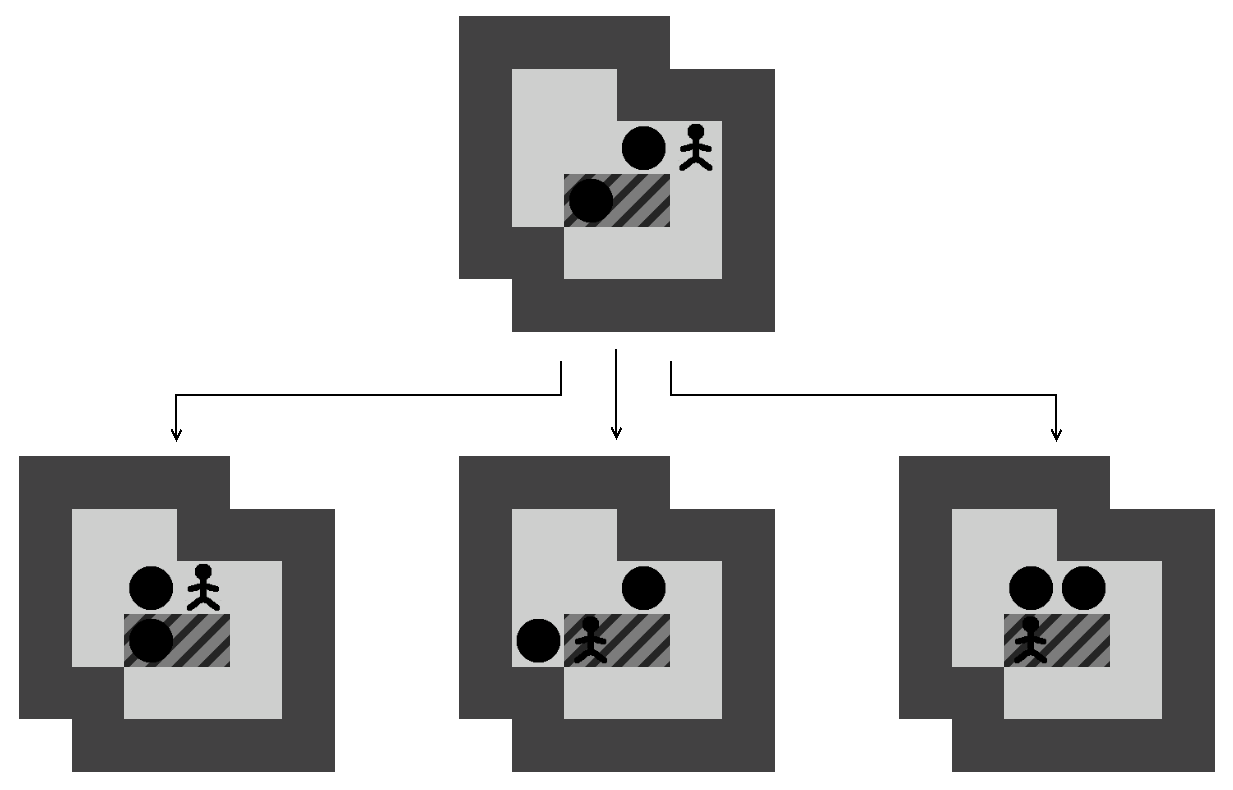
Afin de limiter la taille de l'arbre de recherche, ce ne sont pas les mouvements du pousseur qui sont pris en compte mais les poussées des caisses. Les transitions entre un état et ses fils correspondent donc chaque fois à une succession de mouvements suivie d'une poussée comme indiqué sur la Figure 4.1. Cette couche d'abstraction nous permet d'arriver plus vite à un état solution mais ne nous garantit pas l'obtention de la solution optimale en terme de mouvements, seulement celle en terme de poussées.
Nous avons vu qu'un état est représenté par la position du pousseur et des caisses. Les positions des murs et des goals ne sont pas stockées avec l'état car elles ne varient pas. Étant donné l'abstraction du nombre de mouvements du pousseur, nous pouvons généraliser la définition d'un état par :
- La position des caisses.
-
Les positions qui peuvent être atteintes par le pousseur sans devoir pousser de caisses.
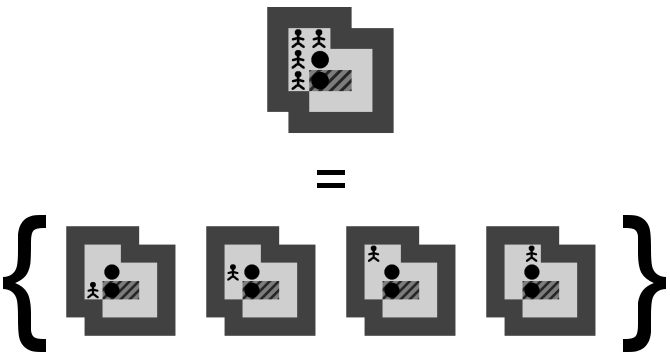
La position exacte du pousseur importe peu. Tant qu'il reste dans un ensemble de positions atteignables sans la moindre poussée, les futures poussées possibles à partir de cet état seront les mêmes. En généralisant la position du pousseur de la sorte, nous évitons de multiplier dans notre arbre les états qui ont des descendances identiques. Nous réduisons ainsi les branches potentielles à explorer. La Figure 4.2 montre bien qu'un seul état généralisé correspond simultanément à plusieurs états sans perdre d'information et donc l'optimalité de la solution.
4.2 État de l'art
Depuis l'apparition de Sokoban, celui-ci a été le sujet de nombreuses recherches qui ont conduit à la conception de solveurs. L'efficacité de ces solveurs est à chaque fois mise à l'épreuve sur le même ensemble de 90 niveaux. Cet ensemble regroupe les 50 niveaux de la première version de SokobanOriginalHighScore (Pas d'année) ainsi que 40 niveaux postérieursExtraHighScore (Pas d'année) dont la paternité semble appartenir à Joseph L Traub.
Si un solveur réussit à résoudre plus de niveaux qu'un autre, cela ne signifie pas qu'il est globalement meilleur. En effet, notre ensemble de tests ne représente qu'une infime partie de l'ensemble des niveaux existants ou potentiels. Il constitue néanmoins une bonne base pour estimer l'efficacité d'un nouveau solveur.
La suite de ce chapitre détaille les avancées des solveurs les plus prometteurs de ces dernières années. Certaines notions abordées pourront paraître obscures pour un lecteur non averti. Qu'il se rassure, elles seront détaillées dans la suite de ce document.
Rolling Stone
Le solveur Rolling Stone est certainement celui qui est le plus documenté à ce jour. Il provient de l'Université d'Alberta, Canada. Des recherches y ont été faites entre 1997 et 2001 et il en résulte une Thèse écrite par Andreas JunghannsJunghanns (1999) et de nombreuses publications d'articles sur des méthodes testées et plus ou moins efficaces. L'utilisation d'une méthode intelligente de parcours de l'arbre de recherche (IDA*) permet d'assurer l'optimalité de la solution en terme de poussées d'un niveau. De plus, de nombreuses méthodes de détection de deadlocks et de pénalités sont utilisées et réduisent considérablement la taille de l'arbre de recherche.
Ces techniques, associées à une quantité d'optimisations, permettent à Rolling Stone, programmé en C, d'obtenir les solutions optimales de 57 niveaux sur les 90 testés.
Talking Stone
Le solveur Talking Stone est plus récent et date de 2006. Il a été créé par François Van Lishout à l'Université de Liège, Belgique, dans le cadre d'un DEA en Sciences AppliquéesVan Lishout (2006). Une nouvelle approche Multi-Agent est utilisée dans le but de faire interagir les éléments principaux du jeu – les caisses – entre-eux avec un objectif commun. F. Van Lishout est parvenu à trouver un algorithme permettant de résoudre les niveaux lorsque ceux-ci appartiennent à une certaine sous-classe prédéfinie. L'idée principale est qu'un niveau appartient à cette sous-classe si on peut trouver une association caisses-goals permettant de mettre, tour à tour, chaque caisse sur son goal. Cette méthode a cependant très vite montré ses limites car un seul niveau a ainsi pu être résolu.
L'évolution proposée est d'appliquer un parcours IDA* de l'arbre de recherche à la manière de Rolling Stone afin de trouver un état qui pourrait répondre aux conditions de la sous-classe. Grâce à cette amélioration, le solveur permet de résoudre 9 des 90 niveaux de base mais en utilisant très peu d'optimisations proposées par Rolling Stone. Un autre avantage est qu'il permet d'utiliser moins d'espace mémoire pour trouver une solution. Talking Stone est programmé en Scheme.
Talking Stone (2)
Un autre solveur est apparu l'année suivante à Liège, toujours en Scheme et reprenant les principes de base de Talking Stone. Il a été créé par Jean-Noël Demaret dans le cadre de sa Deuxième LicenceDemaret (2007) et reprend l'approche Multi-Agent en l'améliorant et en insérant des optimisations propres au Sokoban. Il concrétise l'intérêt de l'approche de Talking Stone en résolvant 54 niveaux tout en laissant une légère marge de progression.
- Le premier détermine l'ordonnancement des goals en analysant la situation de jeu initiale.
- Le deuxième a pour objectif de placer les caisses sur les goals dans l'ordre défini par l'ordonnancement.
-
Le troisième est responsable de la résolution d'un sous-problème consistant à placer une caisse sur son goal.
Etant donné que cette façon de procéder repose sur un ordonnancement des goals qui dépend d'une certaine heuristique, les solutions trouvées seront souvent non-optimales. De quelques poussées à plusieurs dizaines de poussées supplémentaires pour résoudre certains niveaux, tel est le prix à payer pour trouver une solution. La rapidité du solveur pour en trouver une est néanmoins un atout indéniable.
Sokoban Automatic Solver
Le solveur Sokoban Automatic Solver est certainement celui qui est le plus puissant à ce jour. Il est toujours en développement et sa première version semble dater de 2003. Malheureusement, il est non documenté et son code n'est pas disponible. Il est créé par le Japonais Ken'ichiro Takahashi et la version 7.2.2 de janvier 2008Takahashi (Pas d'année) permet de résoudre 86 des 90 problèmes proposés, ce qui est réellement impressionnant. Les solutions trouvées ne sont pas optimales ce qui laisse supposer qu'il utilise des heuristiques très précises pour réduire la taille de l'arbre de recherche.
4.3 Contributions
Aborder la conception d'un solveur n'est pas une chose aisée. Le domaine est vaste et a déjà été le sujet de nombreuses recherches. Pour éviter de se contenter de ce qui a déjà été trouvé, il est important de se poser régulièrement la question “quelle fonctionnalité puis-je ajouter pour essayer d'obtenir de meilleurs résultats ? ” ou “comment puis-je améliorer un aspect déjà existant ?”. De plus, un tri doit être fait parmi les méthodes existantes car toutes les implémenter laisserait peu de temps pour des innovations personnelles.
Cette section présente les choix qui ont été faits dans le cadre de notre solveur ainsi que les nouvelles fonctionnalités et améliorations proposées.
Optimalité des solutions
Avant même de commencer à concevoir un solveur, il convient de faire certains choix qui conditionneront les méthodes utilisées durant tout le développement. Un aspect mis en évidence par la précédente section concerne l'optimalité des solutions.
Les recherches menées à l'Université d'Alberta ont toujours respecté l'optimalité des solutions en évitant de supprimer des branches de l'arbre de recherche qui pourraient éventuellement contenir la solution optimale. À l'inverse, à l'Université de Liège, l'optimalité n'était pas une contrainte et de puissantes heuristiques ont pu être utilisées pour accélérer la découverte d'une bonne solution mais qui ne sera pas nécessairement optimale.
Nous avons fait le choix de respecter l'optimalité des solutions. Les techniques les plus avancées que nous utiliserons proviendront donc, principalement, de ce qui a été fait dans le cadre de Rolling Stone. Cependant, certaines techniques générales qui interviennent lors de la construction de l'arbre de recherche sont communes à toutes les recherches. C'est le cas des doublons et des deadlocks. Nous en parlerons de manière approfondie dans les chapitres suivants.
Si l'optimalité des solutions a autant d'importance à nos yeux, c'est avant tout parce qu'il est plus facile de passer d'un solveur optimal à un solveur non-optimal, en ajoutant certaines heuristiques, que l'inverse. De plus, parmi les solveurs dont les recherches ont été publiées, c'est malgré tout celui qui conserve l'optimalité qui obtient le plus de solutions.
Une autre raison à ne pas perdre de vue est que la mémoire vive était, il y a quelques années, une limitation qui poussait les programmeurs à réduire la taille de l'arbre de recherche. De nos jours, avec seulement 700mo de ram allouées, il est possible de travailler avec un arbre de recherche de plus de 5 millions de nœuds. Un tel arbre devrait nous permettre de trouver les solutions optimales d'une bonne partie des niveaux de tailles et difficultés raisonnables. Bien entendu, travailler dans le cadre de solutions optimales ne signifie pas que nous ne devons pas tenter de réduire la taille de l'arbre de recherche. Les méthodes utilisées, cependant, ne supprimeront que les branches dont on peut affirmer qu'elles n'aboutiront pas à une solution optimale.
Zone
Une zone est une technique qui consiste à représenter un ensemble de positions dans le niveau. Le concept de zone est apparu très tôt dans l'élaboration de notre solveur. Initialement prévu pour alléger l'espace de stockage de l'arbre de recherche, en utilisant des bits pour stocker les positions des caisses, il a très vite montré son efficacité dans bon nombre de situations. Il permet, entre autres, de trouver toutes les caisses que le pousseur peut déplacer dans un état en seulement quelques opérations sur des entiers. Étant donné que ces optimisations concernent les aspects les plus élémentaires d'un solveur, et donc les plus courants, elles s'avèrent très efficaces dans la pratique. Le concept de zone sera développé dans la Section 5.5.
De plus, les zones permettent de représenter tous les ensembles de positions de la même manière et avec les mêmes outils. Ces ensembles de positions peuvent concerner les caisses, les goals, les positions du pousseur et bien d'autres situations que nous verrons plus tard. Cette façon uniforme de procéder permet une certaine abstraction qui permet de mieux cerner certains problèmes rencontrés.
Deadlock
Concrètement, un deadlock est un état dont on peut affirmer, par l'une ou l'autre méthode (cf. Chapitre 8), qu'il ne mènera pas à une solution. En d'autres mots, cet état est la racine d'un sous-arbre de l'arbre de recherche qu'il faut éviter de créer, au risque de faire croître inutilement la taille de l'arbre et augmenter le temps de résolution du problème.
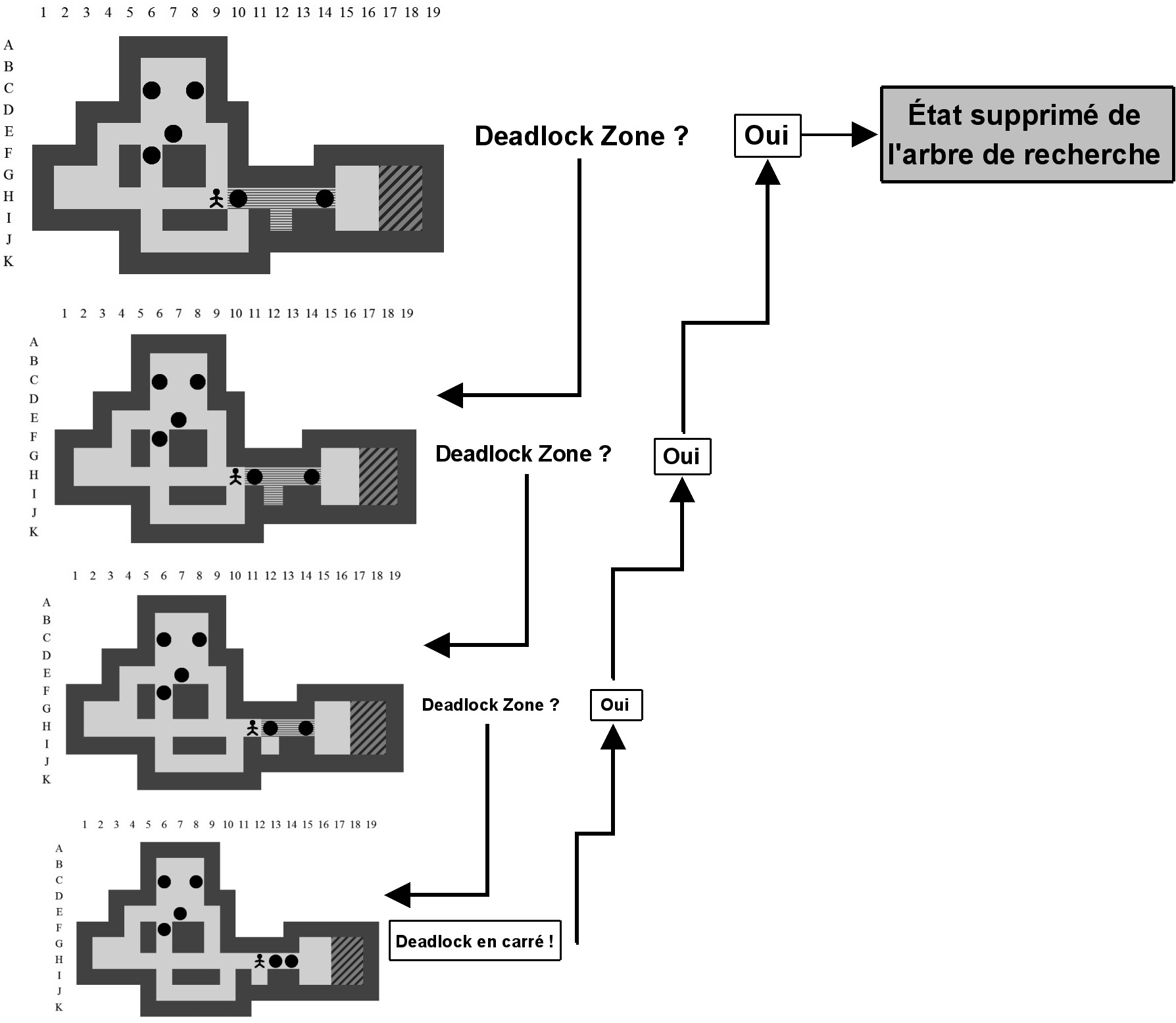
Un certain nombre de techniques efficaces ont été implémentées à partir de méthodes décrites dans la Section 4.2. Nous avons ajouté à celles-ci une nouvelle méthode permettant d'étendre la notion de deadlock à celle de deadlock zone. Cette méthode découle d'observations effectuées lors de l'utilisation du solveur sur certains niveaux et est décrite dans la Section 8.2.2.
Tables de coût et pénalités
Une des méthodes les plus efficaces pour accélérer la recherche de solutions optimales consiste à estimer le nombre de poussées restantes pour qu'un état aboutisse à un état solution. Plus l'estimation est précise et plus les chances d'arriver rapidement à une solution augmentent. Afin d'estimer au mieux cette valeur, deux outils s'offrent à nous :
-
les tables des coûts qui définissent, pour chaque position d'un niveau, le nombre de poussées nécessaires pour pousser une caisse se trouvant sur cette position vers chacune des autres positions.
-
Les pénalités que l'on peut assigner à certains sous-ensembles de caisses qui se gênent mutuellement pour arriver à une solution. Il faut donc infliger un coût supplémentaire, et donc une pénalité, à tous les états qui comprennent ce sous-ensemble.
Bien que ces outils ont déjà été utilisés dans de précédents travaux, un soin tout particulier a été apporté quant à leur implémentation. Plus les coûts et pénalités seront précis et plus le solveur sera performant. Nous avons laissé peu de place à l'approximation et nombre de cas particuliers ont été envisagés.
Pré-traitement / Post-traitement
Nous définissons le pré-traitement par le travail effectué par le solveur sur un niveau avant de commencer à construire l'arbre de recherche. Le post-traitement, à l'opposé, est le travail effectué par le solveur sur un niveau après la construction de l'arbre de recherche. Ces techniques, idéalement, recherchent des résultats intermédiaires et les enregistrent dans un fichier. Ce fichier sera ensuite chargé lors de la prochaine utilisation du solveur et utilisé pour accélérer l'obtention de résultats.
Dans les précédentes recherches de la Section 4.2, il semble n'y avoir eu que quelques cas de pré-traitement, notamment dans le cadre de l'utilisation de Deadlock Tables dans Junghanns (1999). Peut-être étaient-ils passés sous silence mais utilisés dans la pratique. Peut-être également que l'une des contraintes était de pouvoir recalculer les informations utiles à la volée. Quoi qu'il en soit, nous pensons que ces techniques sont intéressantes car facultatives et persistantes. Facultatives car il est possible d'utiliser le solveur sans utiliser de pré-traitement ni de post-traitement. Persistantes car une fois un traitement effectué, il peut être chargé instantanément lors d'une prochaine utilisation du solveur et être utilisé tel quel ou complété.
Langage de programmation
Par le passé, les principaux solveurs ont été programmés en C (Université d'Alberta) et en Scheme (Université de Liège). Le langage C possède la particularité d'être de bas niveau, proche de la machine et très rapide. Le langage Scheme, au contraire, se situe à un plus haut niveau et met l'emphase sur les avantages de la programmation fonctionnelle. Ce dernier choix est judicieux pour la construction d'arbres car très porté sur l'utilisation de listes, et celles-ci sont fréquentes dans ce domaine.
Nous avons fait le choix de travailler en C++. Ce choix est avant tout motivé par la vitesse d'exécution de celui-ci. En effet, c'est d'un solveur dont il s'agit et la vitesse d'exécution joue donc un rôle crucial. Le C++, par rapport au C, est un rien plus lent mais comprend le paradigme objet qui est une avancée certaine en terme de facilité de programmation et de réutilisation. Le Java, qui est également orienté objet, a très vite été rejeté à cause de sa lenteur provoquée par la machine virtuelle ainsi que sa gestion aléatoire et peu flexible de la mémoire.
Le seul avantage apporté par Java aurait été sa portabilité. Ce n'est pas un problème car notre implémentation en C++ a été prévue pour être compilée et fonctionner correctement sur les différentes plates-formes que sont Linux, MacOS et Windows.
Un autre avantage de C++ est qu'il permet d'effectuer des opérations binaires sur les entiers. Ceci va nous aider à stocker efficacement l'arbre de recherche en utilisant le principe des zones.
Chapitre 5 Prérequis
Pour appréhender correctement les différentes constructions possibles d'un arbre de recherche, nous devons commencer par bien assimiler certains concepts de base. Nous avons choisi une approche qui va du plus général (l'algorithme principal) au plus particulier afin de bien comprendre l'intérêt de certaines structures élémentaires qui seront utilisées tout au long de ce document.
5.1 Algorithme principal
Le fonctionnement principal du solveur est détaillé dans l'Algorithme 1. L'implémentation proposée, bien que de haut niveau et très simplifiée, présente les mécanismes les plus importants d'un tel programme. Pour pouvoir créer l'arbre de recherche, on utilise une liste d'attente, dont le fonctionnement sera décrit dans la Section 5.4.
-
initialisation(niveau) : avant de pouvoir créer l'arbre de recherche, nous avons besoin d'initialiser plusieurs éléments dont l'état initial : celui pour lequel la disposition des caisses correspond exactement à celle du niveau. Cet état sera inséré dans la liste d'attente en tout premier lieu afin d'être introduit comme racine de l'arbre de recherche. Les autres initialisations correspondent aux structures de données qui seront utiles par la suite telles que les tables de hachage, les zones de deadlocks ou les zones de goals.
-
premierNoeudDeListe() : Récupère le premier nœud (et donc un état, cf. Section 5.3) de la liste d'attente.
-
estSolution(noeud) : Teste si l'état contenu dans le nœud est solution en vérifiant que toutes les caisses se trouvent sur des goals.
-
chercheEnfants(noeud) : à partir d'un nœud, retourne la liste des nœuds considérés comme enfants, c'est-à-dire à une poussée de l'état contenu dans le nœud tel que représenté sur la Figure 4.1.
-
dejaExistant(noeud) : indique si un nœud existe déjà dans l'arbre de recherche.
-
deadlock(noeud) : indique si l'état contenu dans le nœud est un deadlock et donc provoque une impasse dans l'arbre de recherche.
-
ajouteDansArbre(noeud) : ajoute un nœud à sa place dans l'arbre de recherche.
-
ajouteDansListe(noeud) : ajoute un nœud dans la liste d'attente. De l'endroit où le nœud sera ajouté dépendra la méthode de création de l'arbre de recherche.
-
supprime(noeud) : supprime un nœud. Il ne sera conservé ni dans l'arbre de recherche, ni dans la liste d'attente ou la table de hachage.
- recupereChemin(noeud) : à partir du nœud solution, permet de remonter vers la racine de l'arbre de recherche en évoluant de père en père. Cela permet de déduire, via un algorithme non-trivial, le chemin solution emprunté par le pousseur à partir de la racine.
5.2 État
Un état est représenté par la position du pousseur et par celle des caisses. Grâce à la notion d'état généralisé, la position du pousseur est définie comme l'ensemble des positions que le pousseur peut atteindre dans l'état sans devoir pousser de caisses.
Les différentes données contenues dans un état, qu'elles soient relatives aux caisses ou au pousseur, ne sont rien de plus que des ensembles contenant des positions. Les représentations peuvent donc être faites à l'aide d'un même outil. Cet outil, la zone, permet de gérer facilement différents ensembles de positions (cf. Section 5.5).
Comme nous l'avons signalé dans la Section 4.1, la structure d'un état ne doit pas contenir d'information relative aux positions des goals et des murs. Celles-ci sont stockées au début de la résolution d'un niveau et ne sont plus recalculées par la suite.
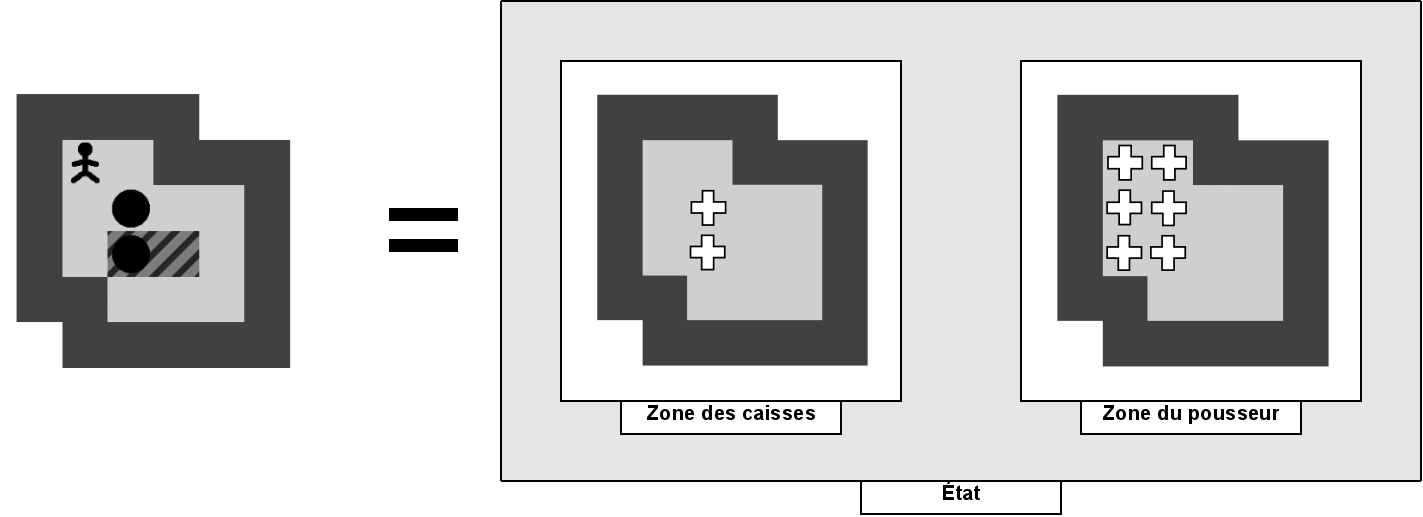
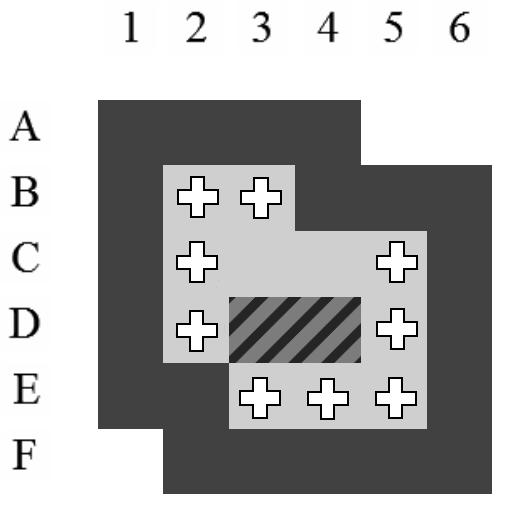
La Figure 5.1 représente la structure d'un état tel qu'il est stocké en mémoire. Les croix représentent les positions qui sont utilisées respectivement par les caisses et par le pousseur. La zone du pousseur comprend également les caisses voisines de son champ d'action. Nous verrons dans la section 5.5 pourquoi nous procédons de la sorte.
5.3 Nœud
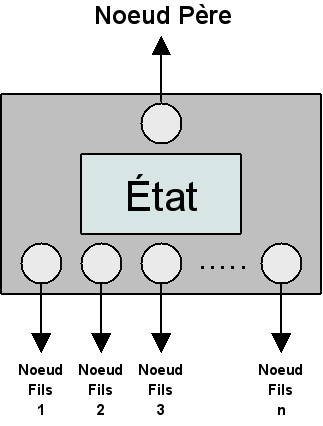
Un nœud est un élément qui englobe un état et qui lui permet de se greffer sur un arbre de recherche existant. Il donne à l'état la possibilité d'interagir avec les autres états présents dans l'arbre de recherche. Comme on peut le voir sur la Figure 5.2, le nœud contient un état ainsi que des références vers son nœud père et ses nœuds fils.
Dans la suite de ce document, le terme “nœud” sera utilisé pour parler d'un état lorsque la volonté sera d'insister sur sa position et ses relations au sein de l'arbre de recherche.
5.4 Liste d'attente
La liste d'attente permet de stocker les nœuds qui n'ont pas encore été traités. Un nœud traité est un nœud pour lequel nous avons trouvé et placé les enfants dans l'arbre de recherche et dans la liste d'attente si ceux-ci s'avèrent utiles. Le parcours de l'arbre de recherche dépend de la manière dont nous manipulons les nœuds en attente dans cette liste.
La liste d'attente est une structure de données dans laquelle nous pouvons ajouter et retirer des éléments. La structure de données la plus simple dans le cadre de la construction d'un arbre de recherche est la liste doublement chaînée. Le concept d'une liste dont chaque élément est relié à son prédécesseur et à son successeur permet de gérer très facilement des structures de types LIFO (Last In, First Out) ou FIFO (First In, First Out).
Dans d'autres cas de constructions plus complexes, une contrainte impose que la liste reste triée. Chaque nœud possède alors un certain coût et la liste doit conserver un ordre prédéfini. Pour cela, l'insertion doit veiller à positionner les nouveaux éléments aux endroits adéquats. Les listes doublement chaînées auraient pu fonctionner dans un tel cas mais avec une complexité qui aurait été désastreuse en cas d'insertion triée ( où est le nombre d'éléments dans la liste). Nous avons donc opté pour une structure plus efficace : le tas (cf. Section 6.3.1).
5.5 Zone
5.5.1 Objectif
Une zone a pour objectif de pouvoir représenter et manipuler rapidement n'importe quel ensemble de positions dans un niveau. Les ensembles suivants peuvent ainsi être représentés à l'aide de zones :
- Les positions des caisses.
- Les positions du pousseur dans l'état généralisé.
-
Les positions des goals.
Dans la pratique, il existe d'autres ensembles que nous manipulerons, entre autres pour la gestion des deadlocks. Ceux-ci seront introduits en temps voulu.
Les zones ne peuvent représenter que les positions qui se situent à l'intérieur d'un niveau par rapport aux murs. En d'autres mots, les positions sur lesquelles le pousseur et les caisses peuvent évoluer. La Figure 5.3 représente l'ensemble des positions qui sont représentées par une zone sur ce niveau. Comme illustré, les positions sont numérotées ligne par ligne, en partant du coin supérieur gauche.
- La zone des caisses :
- La zone du pousseur dans l'état généralisé (cf. Section 5.2) :
- La zone des goals :
Les zones permettent aux éléments du jeu de Sokoban d'être manipulées comme des ensembles à l'aide d'opérations qui comprennent l'intersection et l'inclusion.
5.5.2 Implémentation
Tout l'intérêt d'une zone est de pouvoir être représentée par un nombre binaire. Dans l'exemple de la Figure 5.3, nous voyons qu'une zone est définie par 23 positions. Ces positions peuvent toutes être représentées par un bit. Le bit vaudra 1 si la position est comprise dans l'ensemble et si elle ne l'est pas.
En posant , le nombre d'éléments dans une zone, et en admettant que la taille d'un entier soit de 32 bits, il est nécessaire d'utiliser entiers pour représenter chacune des zones d'un niveau. Les bits en excès pour la représentation des positions seront tous affectés à 0.
Voici les représentations binaires des 3 zones décrites dans la section précédente ainsi que les valeurs entières correspondantes :
- La zone des caisses :
- La zone du pousseur dans l'état généralisé (cf. Section 5.2) :
- La zone des goals :
Nous avons donc réduit la représentation d'un ensemble de positions à une simple valeur entière. Ceci s'avère très économique pour la consommation de mémoire car chaque état ne contiendra que deux zones (cf. Section 5.2) et donc seulement 2 valeurs entières par tranche de 32 positions dans le niveau.
5.5.3 Tables de traduction
Selon notre définition des zones, il n'est pas possible d'y inclure de mur car ceux-ci ne sont pas compris dans les positions couvertes par la zone. Il va donc être nécessaire d'utiliser deux méthodes pour décrire les positions des éléments du jeu :
-
Le positionnement absolu : il permet de couvrir toutes les positions d'un niveau sans exception. Chaque position est référencée par l'intersection entre une ligne (lettre) et une colonne (nombre). Cette méthode permet de situer les éléments fixes d'un niveau comme le murs ou les positions extérieures.
-
Le positionnement relatif à la zone : il permet de couvrir les positions comprises dans la zone. Il sera utilisé pour situer les éléments dans une zone tels que les caisses ou les positions du pousseur. Cette méthode est essentiellement utilisée dans les interactions avec un état.
Nous avons deux méthodes différentes pour faire référence à une même position. Ceci peut poser problème lorsque l'on veut, par exemple, vérifier qu'une caisse d'un état (positionnement relatif à la zone) est située à côté d'un mur (positionnement absolu).
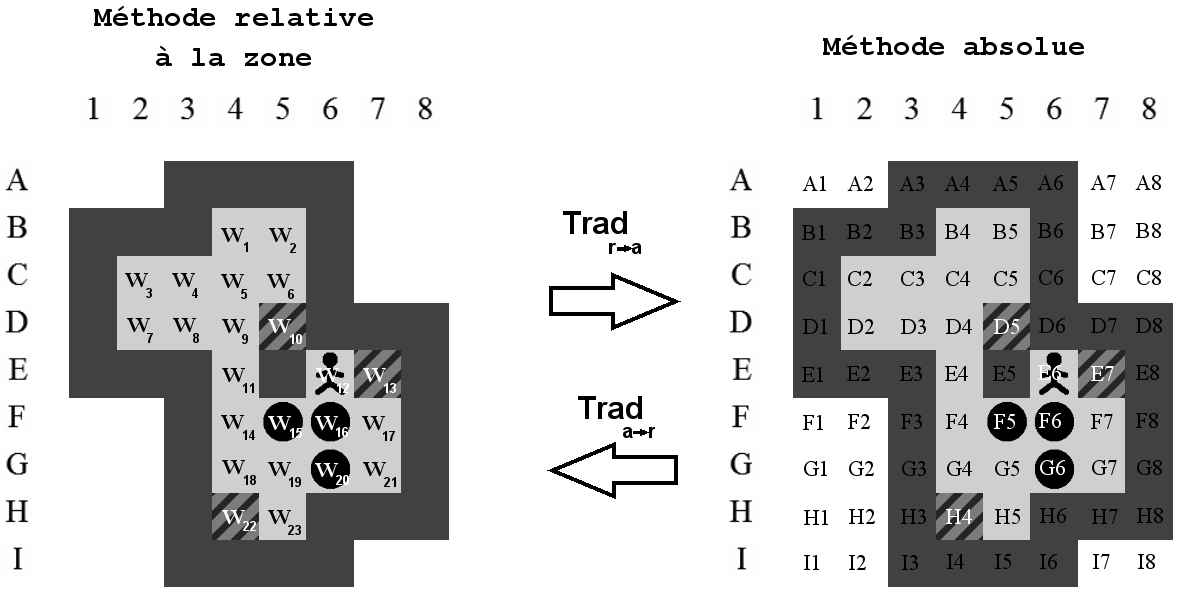
Pour éviter ce problème, deux tables de traduction et sont créées. Celles-ci ont la propriété d'associer une position relative à chaque position absolue et vice versa tel qu'illustré sur la Figure 5.4. Dans le cas où aucune position relative ne correspond à une position absolue, la table de traduction retournera pour bien indiquer l'impossibilité. C'est le cas de qui retournera pour bien montrer l'impossibilité de représenter cette position par la méthode relative.
5.5.4 Opérations
En plus d'être peu consommatrices de mémoire, les zones permettent de réduire le nombre de calculs lors de la résolution d'un niveau. Les opérations les plus fréquentes sont détaillées dans les paragraphes suivants.
Tester si un état est solution
Tester si un état est solution consiste à comparer la zone des caisses de l'état avec la zone des goals calculée une fois pour toutes à l'initialisation de la résolution. C'est-à-dire une unique comparaison entre les entiers qui représentent les deux zones ce qui, sur la Figure 5.3, donne simplement . Dans le cas où il y a plus de goals que de caisses, il faudra utiliser l'inclusion telle que décrite plus loin dans cette section.
Si nous avions enregistré individuellement les positions de chacune des caisses, nous aurions dû vérifier, pour chaque état rencontré, si elles se situent toutes sur des goals ou non.
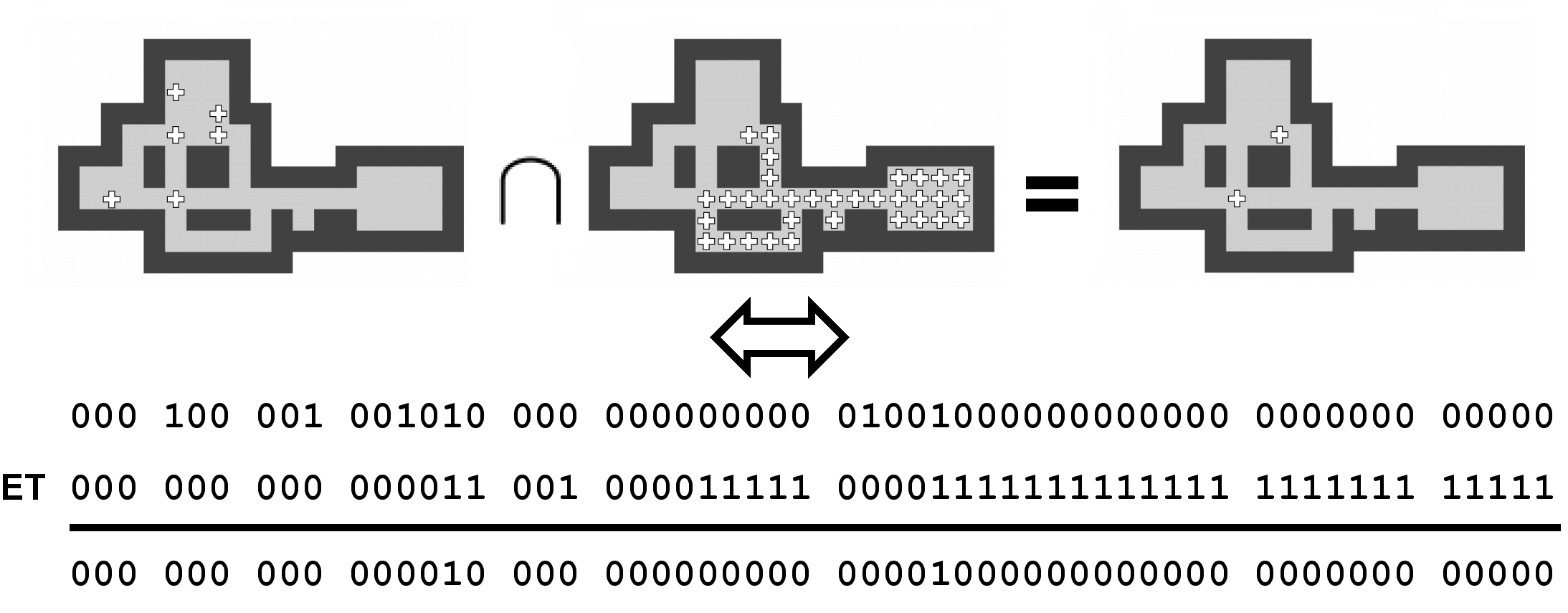
Trouver les poussées potentielles
Dans notre implémentation, la décision a été prise d'ajouter à la zone du pousseur toutes les caisses qui sont voisines aux positions que le pousseur peut atteindre. Cela ne change en rien la quantité d'informations contenues dans un état mais augmente les possibilités d'utilisation de celui-ci. En effet, cette représentation de la zone du pousseur permet de trouver, en une seule opération, toutes les caisses que le pousseur peut atteindre et donc potentiellement déplacer.
Il suffit, comme la Figure 5.5 le montre, de rechercher l'intersection entre les deux zones. Concrètement, cela consiste à appliquer une opération binaire ET entre les représentations de la zone du pousseur et de la zone des caisses. On obtient ainsi une nouvelle zone contenant la position des caisses que le pousseur peut atteindre. On pourra ainsi travailler directement sur un sous-ensemble de caisses, ce qui diminuera la quantité de calculs nécessaires lors de la création des états fils d'un nœud de l'arbre de recherche.
Tester l'inclusion
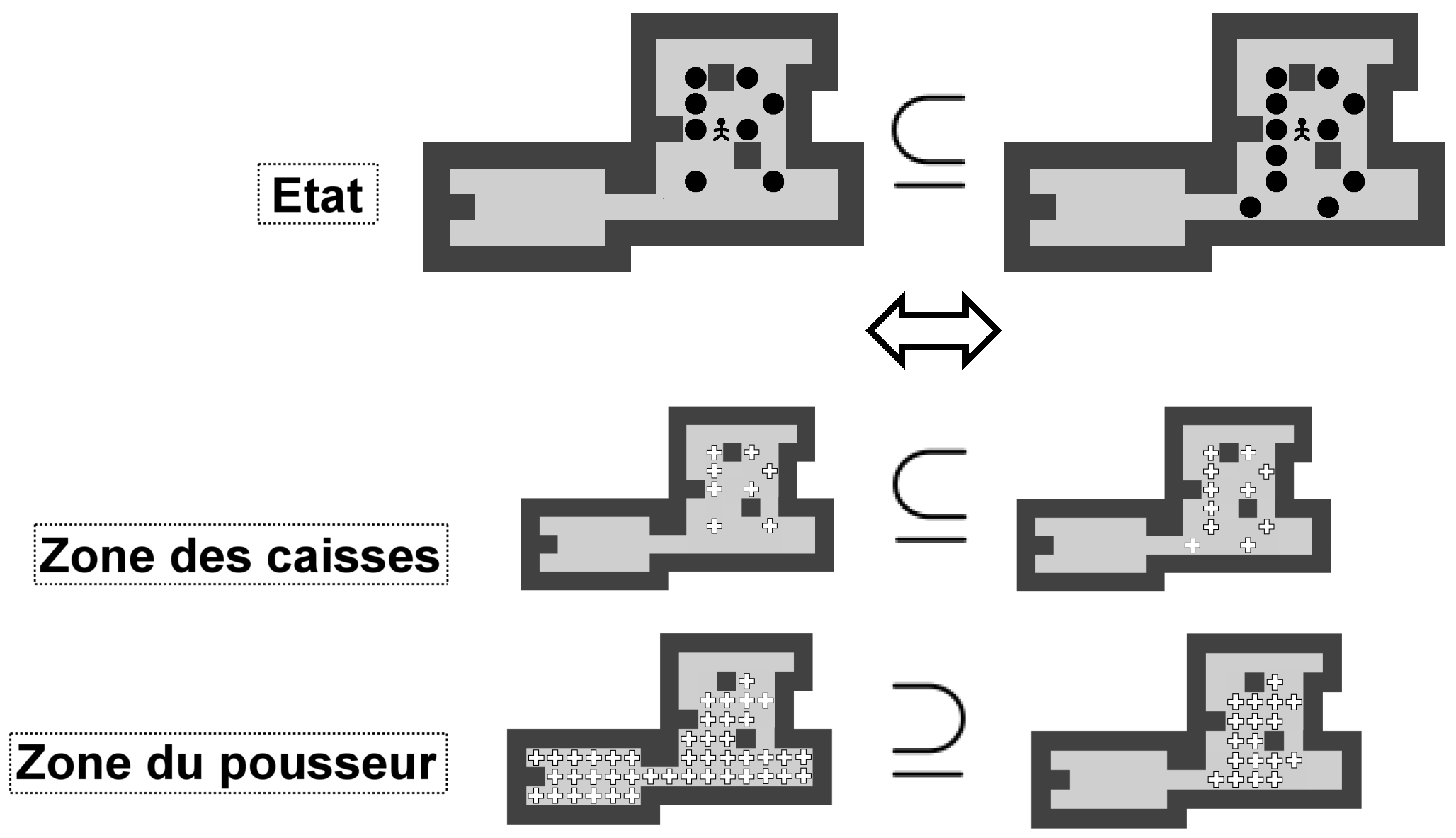
Il est souvent nécessaire de tester si un état est inclus dans un autre état. Pour que avec et des états relatifs au même niveau, il faut que les deux conditions suivantes soient respectées :
-
: toutes les positions de la zone des caisses de l'état doivent appartenir à la zone des caisses de l'état .
-
: toutes les positions de la zone du pousseur de l'état doivent appartenir à la zone du pousseur de l'état .
Le fait que ce soit la zone du pousseur de l'état B qui doit être contenue dans celle de l'état A va à l'encontre d'une première intuition. Il faut cependant prendre en compte, comme représenté sur la Figure 5.6, que moins un état possède de caisses, plus la zone du pousseur sera grande. Dans un état sans caisses, la zone du pousseur représenterait toutes les positions de celui-ci.
À l'aide des zones, tester si , où et sont des zones d'un même niveau, est assez simple. Il suffit d'appliquer à la manière de la Figure 5.5 et ensuite de tester la condition . Si la condition est vérifiée, alors , sinon . Un tel test est donc très rapide car il ne concerne que des opérations élémentaires portant sur des entiers. À chaque opération sur un entier, ce sont 32 positions qui sont testées à la fois.
Tester l'intersection
Il est parfois nécessaire, entre autres pour la détection des deadlocks à une caisse (cf. Section 8.1), de tester si l'intersection entre deux zones est vide ou non.
La technique est fort semblable à celle utilisée pour trouver les poussées potentielles. Il faut commencer par rechercher où et sont deux zones d'un même niveau. La valeur obtenue en est ensuite testée. Si celle-ci vaut (tous les bits qui composent la zone valent ), alors l'intersection entre les deux zones est vide, sinon elle ne l'est pas.
5.6 Doublons
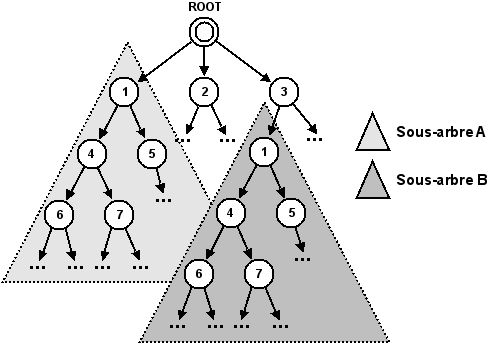
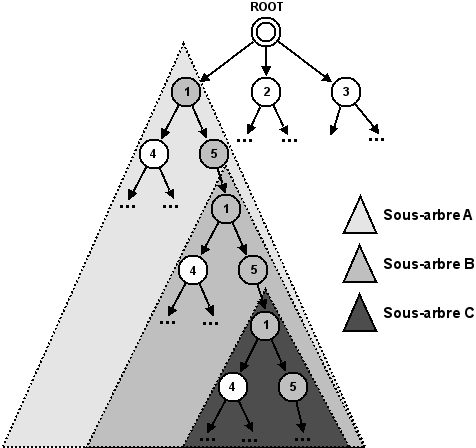
Lors de la création d'un arbre de recherche, il est courant de retrouver plusieurs fois le même état à des endroits différents. En effet, un même état peut être atteint via plusieurs chemins au départ de l'état racine. Étant donné qu'un état possède la même descendance, peu importe l'endroit où il se trouve dans l'arbre de recherche, ce phénomène nous conduira à des sous-arbres qui seront identiques. Si deux sous-arbres identiques apparaissent dans l'arbre de recherche de manière à ce que l'un d'eux soit compris dans la descendance de l'autre, on parlera alors de situation redondante.
Ces problèmes de duplications de sous-arbres et de situations redondantes (cf. Figure 5.7) sont très préoccupants dans un contexte où nous essayons justement de limiter les calculs nécessaires, et donc la taille de l'arbre de recherche, pour trouver une solution.
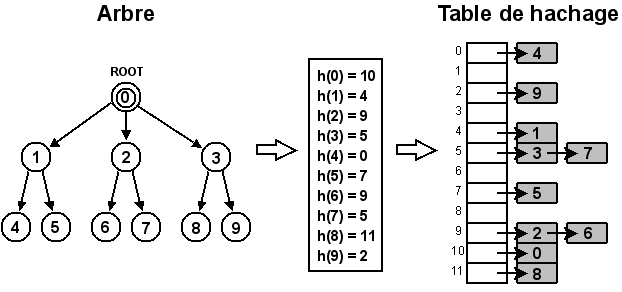
La technique la plus évidente pour éviter de placer deux fois un même état dans l'arbre de recherche consiste à garder en mémoire une copie de chaque état utilisé. La difficulté réside dans le fait qu'il faut utiliser une structure dans laquelle nous pouvons vérifier, à moindre coût, la présence d'un état. Les tables de hachage sont tout à fait appropriées pour ces fonctionnalités. De fait, avec une taille bien pensée et une fonction de hachage performante, une table de hachage permet d'insérer et de récupérer des éléments avec une complexité moyenne en .
La complexité dans le pire des cas est en , où est le nombre d'éléments à stocker . Celle-ci est peu représentative car elle correspond à une fonction de hachage qui renverrait toujours vers la même position de la table, ce qui est le signe d'une fonction de hachage mal adaptée.
Implémentation
Il peut sembler, à première vue, que garder une version de chaque état soit très consommateur de mémoire vive. De fait, garder chaque état utilisé, quand on en utilise plusieurs millions, alourdit considérablement l'espace requis. Cependant, il ne faut pas oublier que les états sont déjà disponibles dans l'arbre de recherche qui est en mémoire. Il est donc inutile de les dupliquer pour les insérer dans la table de hachage alors qu'une simple référence vers le nœud contenant l'état déjà en mémoire est suffisante. En procédant de la sorte, nous évitons une utilisation excessive de la mémoire ram.
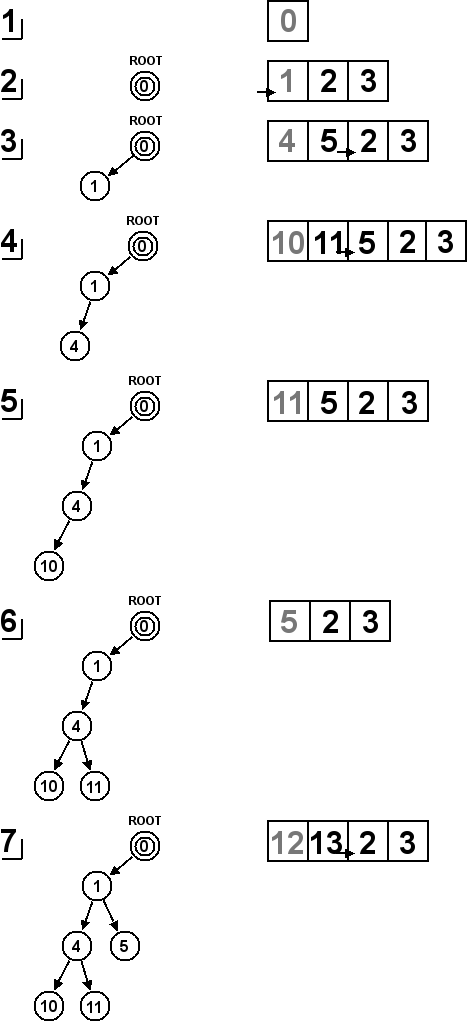
Le fonctionnement d'une table de hachage est très simple. Il consiste en l'utilisation d'un tableau de taille dont toutes les cellules correspondent à des listes chaînées. Posons un nouvel état et une fonction de hachage permettant d'obtenir un nombre naturel à partir d'un état. Un nouvel état sera ajouté au début de la liste chaînée correspondant à la cellule . Si la fonction de hachage et la taille de la table sont définies afin de répartir uniformément les états, chaque liste chaînée ne contiendra en moyenne que quelques éléments. Ceci permettra de conserver une complexité moyenne en pour l'ajout, la suppression ou la recherche d'un état. La Figure 5.8 schématise la manière dont les nœuds de l'arbre de recherche sont ajoutés à la table de hachage.
La fonction de hachage doit avant tout veiller à répartir uniformément les états dans la table. Elle a été implémentée de manière intuitive et son efficacité a ensuite été testée. Notre méthode consiste à additionner tous les entiers utilisés pour représenter un état (cf. Section 5.5) sur lesquels un , où correspond à la taille de la table, est à chaque fois appliqué. Un dernier est ensuite appliqué au total obtenu.
La taille de la table de hachage doit être allouée au début de son utilisation et répondre à certaines conditions pour une utilisation performante. La première est que sa taille corresponde plus ou moins au nombre d'états que nous voulons y stocker. Nous pensons qu'un nombre proche du million représente assez bien notre intention. La deuxième condition est de “choisir un nombre premier n pas trop proche d'une puissance de 2” afin d'éviter des problèmes de diviseurs communs étant donné que nous utilisons une fonction de hachage basée sur une méthode par division. En respectant ces conditions, nous avons choisi une taille de cellules.
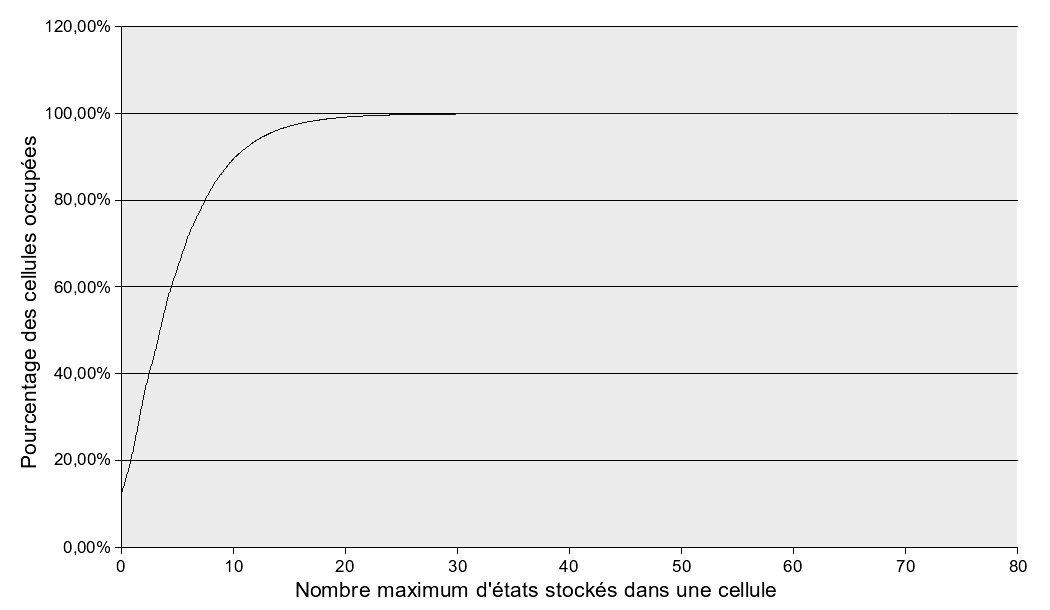
La table de hachage a été testée de manière intensive (cf. Tableau 5.1 et Figure 5.9) avec la création d'un arbre de recherche contenant environ 4250000 nœuds. Les résultats attendus correspondent à une moyenne de 5 éléments par liste chaînée. Les résultats obtenus sont assez concluants car 65% des listes contiennent jusqu'à 5 éléments, 90% des listes contiennent jusqu'à 10 éléments et 99% des listes possèdent 20 éléments ou moins. Sans être exceptionnels, ces résultats ne justifient pas la recherche d'une meilleure fonction de hachage.
Chapitre 6 Parcours
Nous avons vu dans la Section 4.1 que la résolution d'un problème de Sokoban nécessitait la construction d'un arbre de recherche. Le moment est venu de décrire les différentes façons de construire cet arbre. Chacune des méthodes proposées possède ses avantages et inconvénients et diffère essentiellement des autres par l'ordre dans lequel les nœuds dans la liste d'attente seront placés dans l'arbre de recherche.
Dans les exemples qui vont suivre, nous allons utiliser différents algorithmes pour parcourir l'arbre de recherche illustré. Il faut cependant noter que, dans le cadre de notre solveur, nous ne parcourons pas un arbre de recherche qui existe déjà. Dans les faits, nous parcourons un arbre créé dynamiquement selon des règles prédéfinies : création des états fils, détection des deadlocks, des doublons, … Les idées principales restent néanmoins les mêmes dans les deux cas.
6.1 Parcours en largeur
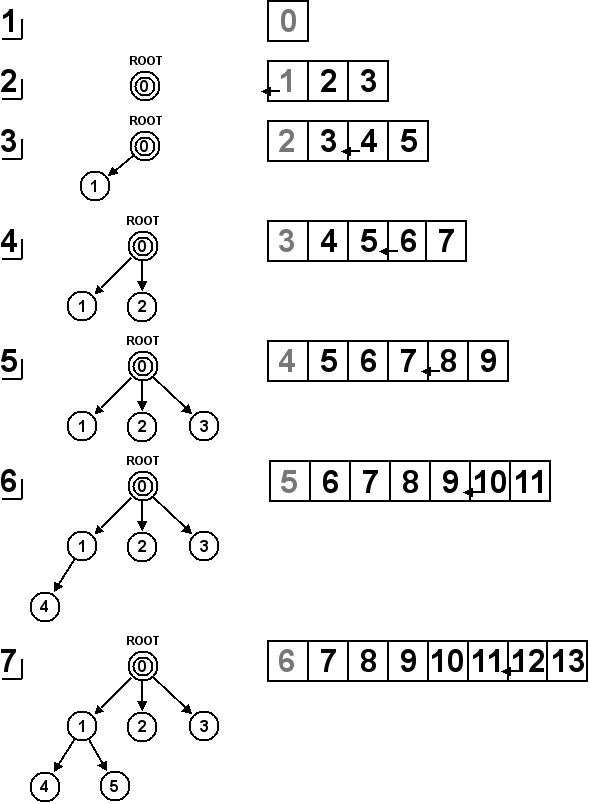
Le parcours en largeur utilise une liste d'attente FIFO (First In, First Out), c'est-à-dire une file, pour traiter les nœuds en attente. De cette façon, les nœuds arrivés en premier dans la liste d'attente seront placés en priorité dans l'arbre de recherche. Étant donné que l'Algorithme 1 utilise toujours le premier nœud de la liste pour le placer dans l'arbre de recherche, la fonction ajouteDansListe(noeud) va insérer chaque nouveau nœud à la fin de la liste chaînée tel qu'illustré sur la Figure 6.2.
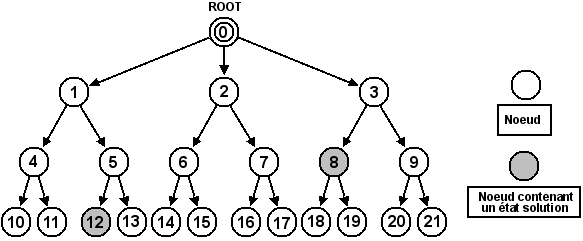
Le parcours en largeur explore en priorité les nœuds les plus hauts de l'arbre de recherche. Du fait que dans notre solveur, chaque saut d'un nœud à un autre corresponde à une seule poussée, nous pouvons en déduire que l'optimalité en terme de poussées de la solution sera atteinte. Sur la Figure 6.1, nous pouvons voir deux nœuds qui contiennent des états solutions. L'une des deux solutions est optimale avec 2 poussées (nœud 8) et l'autre ne l'est pas avec 3 poussées (nœud 12). Avec le parcours en largeur, la solution qui sera trouvée la première sera bien celle qui est optimale.
6.2 Parcours en profondeur
Le parcours en profondeur utilise une liste d'attente LIFO (Last In, First Out), c'est-à-dire une pile, pour traiter les nœuds en attente. De cette façon, les nœuds arrivés en dernier dans la liste d'attente seront placés en priorité dans l'arbre de recherche, privilégiant ainsi les nœuds plus profonds. Étant donné que l'Algorithme 1 utilise toujours le premier nœud de la liste pour le placer dans l'arbre de recherche, la fonction ajouteDansListe(noeud) va insérer chaque nouveau nœud au début de la liste chaînée tel qu'illustré sur la Figure 6.3.
Le parcours en profondeur explore en priorité les nœuds les plus profonds de l'arbre de recherche. Certains nœuds situés au niveau seront ainsi explorés avant que tous les nœuds situés au niveau ne le soient. Une solution non-optimale pourrait donc être trouvée avant la solution optimale. Une telle situation est illustrée avec la Figure 6.1. Si un parcours en profondeur était appliqué sur l'arbre de recherche, le premier nœud solution trouvé serait le 12. Le problème est qu'un autre nœud non exploré, le 8, contient une meilleure solution.
Le parcours en profondeur, contrairement à celui en largeur, ne trouve donc pas la solution optimale sauf si on le laisse explorer tout l'arbre. Il a néanmoins l'avantage de souvent trouver plus vite une bonne solution à un problème de Sokoban. Les solutions ont plus de chance de se trouver dans les nœuds les plus profonds de l'arbre.
6.3 Parcours informé
Le coût peut être basé sur des propriétés de l'état en lui-même ou sur sa position au sein de l'arbre de recherche. La liste d'attente sera triée en fonction de ces coûts, par exemple en positionnant les nœuds dont les coûts sont les plus faibles en tête de liste. Lorsqu'un nouveau nœud est traité, il n'est pas systématiquement inséré en tête ou fin de liste comme c'était le cas auparavant mais à l'endroit exact de la liste qui correspond à son coût. Le parcours de l'arbre de recherche sera alors défini par l'heuristique utilisée pour définir le coût d'un nœud.
L'intérêt d'une telle méthode est que, si les heuristiques sont assez puissantes, il sera possible de construire un arbre de recherche en traitant en priorité les nœuds les plus susceptibles de mener à une solution. Les autres nœuds, moins utiles, seront rejetés en fin de liste. Son plus grand inconvénient est que les heuristiques pourraient éventuellement rejeter une solution, optimale ou non, en estimant à tort que l'état analysé n'est pas digne d'intérêt.
6.3.1 Tas
Si un parcours informé est utilisé en lieu et place d'un parcours en largeur ou en profondeur, il devient nécessaire de changer la structure de la liste d'attente. En effet, une liste doublement chaînée montre ses limites dès que l'insertion triée devient indispensable. Avec une liste chaînée, il n'y a pas d'alternative possible au parcours de toute la liste pour trouver l'emplacement exact où insérer le nouveau nœud, ce qui implique une complexité en .
Le tas semble être une bonne alternative à la liste chaînée. Celui-ci permet une opération d'insertion triée plus souple que celle utilisable dans le cadre d'une liste. Le fonctionnement et l'implémentation proposés d'un tas proviennent de Introduction to Algorithms .
Fonctionnement
Le tas est représenté sous la forme d'un arbre binaire. Il faut différencier l'arbre binaire utilisé pour le tas de l'arbre de recherche qui sert de transition entre les états, ce sont deux arbres dont les rôles sont bien distincts.
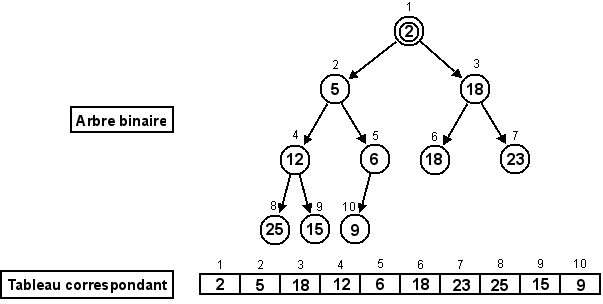
Si l'arbre binaire contient niveaux, alors celui-ci doit être complet sur ses premiers niveaux et le dernier doit être rempli de gauche à droite. Un des aspects les plus pratiques d'un tas est qu'il peut être stocké dans un tableau T tel qu'illustré sur la Figure 6.4. L'arbre binaire correspondant au tas doit respecter un certain ordre dans ses éléments : si A et B sont deux nœuds de l'arbre binaire tels que A est le père de B, alors .
Pour représenter l'arbre binaire d'un tas sous forme d'un tableau T, il suffit d'utiliser certaines relations entre ses cellules. En posant une cellule de , les relations suivantes définissent les positions des cellules qui correspondent à son père et à ses deux fils dans l'arbre binaire :
-
Insertion triée () : insère un nœud dans le tas en fonction de son coût. L'insertion se fait en ajoutant un nœud à la fin du tas et en le remontant jusqu'à la position adéquate à l'aide de la fonction repositionneHaut(T, cell).
-
Extraction () : récupére et supprime le premier nœud du tas, celui dont le coût est le plus petit. La suppression du premier nœud du tas s'effectue en remplaçant le premier nœud par le dernier et en redescendant celui-ci dans le tas jusqu'à la position adéquate à l'aide de la fonction repositionneBas(T, cell).
Incontestablement, l'insertion est plus rapide avec un tas qu'avec une liste chaînée car la complexité dans le pire des cas passe de à . L'extraction, au contraire, devient maintenant dépendante du nombre d'éléments stockés, ce qui n'était pas le cas auparavant. Avec une liste chaînée, il suffisait de déconnecter le premier élément de la liste et de déplacer le pointeur de tête.
Implémentation
Les deux fonctions les plus importantes du tas sont celles que nous avons déjà mentionnées : repositionneHaut(T, cell) (cf. Algorithme 2) et repositionneBas(T, cell) (cf. Algorithme 3). Celles-ci permettent de réorganiser l'arbre binaire respectivement après l'insertion d'un nœud ou la suppression du nœud minimum. Ils permettent aussi, entre autres, de repositionner dans l'arbre binaire un nœud dont le coût aurait été modifié. Cette fonctionnalité aura toute son importance dans le cadre du chapitre suivant : le parcours A*.
6.4 Parcours A*
-
est la distance déjà parcourue par le nœud . C'est-à-dire le coût du meilleur chemin, dans l'arbre de recherche, entre le nœud racine et le nœud .
- est l'estimation de la distance restante à parcourir à partir du nœud pour trouver le nœud solution. où est la distance exacte entre le nœud et le nœud solution. L'estimation doit donc être minorante de la distance réelle.
6.4.1 Fonctionnement
Le parcours A* permet de favoriser les nœuds les plus prometteurs : ceux qui n'ont pas encore parcouru une longue distance et pour lesquels la distance restante devrait être la plus faible.
Dans le cas du Sokoban, le coût représente le nombre de poussées. Le passage entre un nœud parent et un nœud enfant correspond à une unique poussée. est donc facile à calculer et représente la profondeur du nœud dans l'arbre de recherche.
- contient un nœud solution.
- Le nombre de fils d'un nœud quelconque est fini.
-
Il existe un minorant strictement positif de l'ensemble des coûts des arcs.
- Les algorithmes de types A* appliqués à se terminent.
- Un chemin joignant la racine à un nœud solution est trouvé.
-
Le chemin découvert est un chemin de coût minimal dans l'arbre de recherche, entre la racine et l'ensemble des nœuds solutions.
Ce théorème signifie donc que, un nœud de l'arbre de recherche, si est une heuristique admissible et donc minorante de , la solution trouvée sera optimale en terme de poussées.
Si l'estimation de la distance restante était parfaite avec , le parcours A* irait directement de la racine vers le meilleur nœud solution sans s'égarer. Dans les faits, malheureusement, une estimation parfaite est extrèmement difficile à réaliser. La meilleure solution est de multiplier les techniques pour approcher au mieux la valeur de .
6.4.2 Implémentation
Lors du parcours, il a été prévu dans la Section 5.6 de rejeter un état si celui-ci est déjà présent dans l'arbre de recherche. Dans le cas du parcours A*, afin de garder l'optimalité des solutions, il ne suffit plus de rejeter tous les doublons. En effet, deux états identiques peuvent se trouver à deux profondeurs différentes de l'arbre de recherche et possèder deux valeurs différentes pour où est le nœud contenant l'état. Si le nœud dont la valeur est la plus petite, et donc la meilleure, est traité en deuxième lors du parcours, il sera considéré comme doublon et rejeté à tort. Le risque est que ce nœud mène justement à la solution optimale, qui sera alors perdue.
Des manipulations supplémentaires sont donc ajoutées pour, dans le cas de doublons, toujours conserver le nœud dont le coût est le plus bas et réorganiser l'arbre de recherche en fonction. Comme ces manipulations diffèrent en fonction de la présence, ou non, du nœud dans la liste d'attente, un moyen a dû être trouvé pour discerner ces deux types de nœuds.
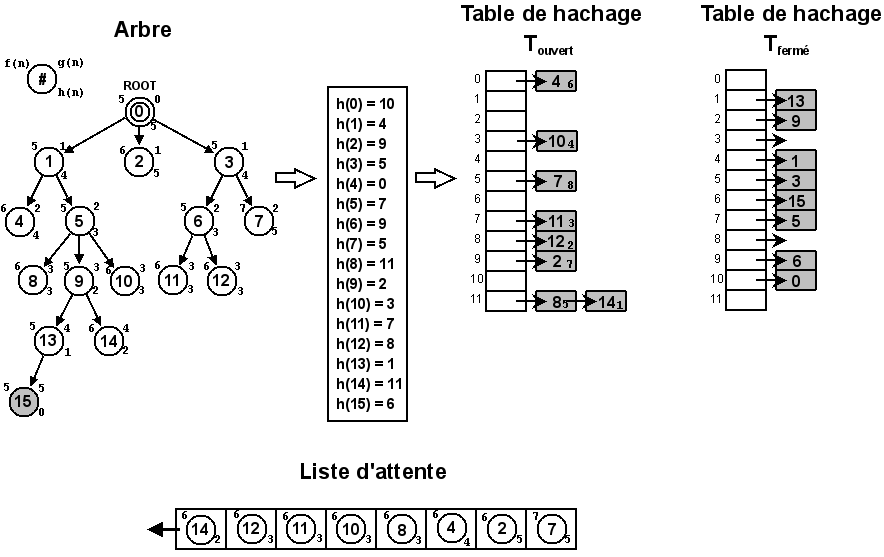
La table de hachage est dédoublée. La première, , est utilisée pour stocker les états ouverts et la seconde, , pour stocker les états fermés. Il est ainsi possible, à partir de l'état contenu dans un nœud, de vérifier rapidement sa présence dans l'une ou l'autre table et d'agir en conséquence.
Il est parfois indispensable de pouvoir accéder directement à l'un des nœuds de la liste d'attente. Le problème est qu'un tas ne permet pas de rechercher efficacement un élément parmi ceux qui sont stockés. La solution la plus simple consisterait à parcourir toutes les cases du tableau correspondant à l'arbre binaire du tas pour trouver celle recherchée. C'est aussi la solution la plus coûteuse car sa complexité serait en où représente le nombre d'éléments stockés dans le tableau.
Une solution plus efficace, qui tire profit de la complexité moyenne en de la table de hachage, consiste à ajouter une nouvelle donnée à chaque élément de qui correspondrait à la position du nœud dans le tas. Cette donnée supplémentaire de la table de hachage devra être mise à jour à chaque manipulation du tas pour que sa valeur reste cohérente.
La fonction dejaExistant(noeud) de l'Algorithme 1, utilisée pour détecter les doublons, est modifiée pour mettre l'arbre de recherche à jour si un doublon s'avère meilleur qu'un nœud déjà présent. L'ancien nœud sera remplacé par le nouveau et les coûts des enfants déjà présents seront adaptés.
L'Algorithme 4 décrit la méthode permettant de gérer efficacement les doublons de manière à conserver l'optimalité de la solution. La première constatation que l'on peut faire est que, dans le cas d'un nouveau nœud qui n'est pas doublon, le fonctionnement est identique à celui des autres parcours. C'est-à-dire que la présence du nœud est déclinée dans la fonction dejaExistant(noeud) et qu'il est ajouté normalement dans l'arbre de recherche sans travail supplémentaire.
Au contraire, dans le cas d'un nœud déjà présent dans l'arbre de recherche, qu'il soit ouvert ou fermé, des manipulations supplémentaires vont devoir être mises en application. Celles-ci se divisent en deux catégories :
Le nouveau nœud est déjà présent dans l'arbre de recherche et
Le nœud présent dans l'arbre de recherche possède, potentiellement, des enfants. Le coût des enfants doit être adapté si la position dans l'arbre de leur ancêtre commun est modifiée. La partie de l'algorithme qui correspond à ce paragraphe est celle qui va de la ligne 2 à la ligne 8.
Si le coût du nouveau nœud est plus grand que celui du nœud présent, l'arbre de recherche n'est pas modifié. À l'opposé, si le coût du nouveau nœud est plus petit, et donc meilleur que celui du nœud déjà présent, on déplace le sous-arbre formé par le nœud présent à l'endroit du nouveau nœud. Les valeurs de de tout le sous-arbre sont ensuite réduites de la différence entre le coût de l'ancien nœud et le coût du nouveau nœud.
-
noeudFerme ← recupere(, noeud) : si noeud existe dans la table de hachage , la fonction retourne la référence vers sa position dans l'arbre de recherche. Si le nœud n'existe pas dans la table de hachage, la fonction existe(noeudFerme) retournera faux.
-
attacheNoeud(noeudFerme, parent(noeud)) : attache noeudFerme au parent du nœud actuellement traité. L'objectif est de déplacer un sous-arbre entier de l'arbre de recherche à un endroit moins profond et donc relatif à un moindre coût.
- reduitCout(noeudFerme, cout(noeudFerme) − cout(noeud)) : réduit le coût du sous-arbre formé de noeudFerme de la différence de valeur, et donc de profondeur, qu'il y a entre l'ancienne position du sous-arbre et la nouvelle.
Le nouveau nœud est déjà présent dans l'arbre de recherche et
Le nœud déjà présent dans l'arbre de recherche n'a pas encore d'enfants et est toujours en attente de traitement dans la liste d'attente (le tas). Si le coût du nœud change, il devra être replacé dans la liste d'attente en fonction de sa nouvelle priorité. La partie de l'algorithme qui correspond à ce paragraphe est celle qui va de la ligne 10 à la ligne 19.
Si le coût du nouveau nœud est plus grand que celui du nœud présent, l'arbre de recherche n'est pas modifié. À l'opposé, si le coût du nouveau nœud est plus petit, et donc meilleur que celui du nœud présent, on modifie la valeur du nœud présent et on l'accroche au père du nouveau nœud. Le nœud présent se situera donc à une position moins profonde de l'arbre. Pour terminer, la position dans le tas du nœud présent est révisée en fonction de son nouveau coût.
-
noeudOuvert ← recupere(, noeud) : si noeud existe dans la table de hachage , la fonction retourne la référence vers sa position dans l'arbre de recherche. Si le nœud n'existe pas dans la table de hachage, la fonction existe(noeudOuvert) retournera faux.
-
cellule ← recupereCelluleTas(, noeud) : grâce à la modification de la table de hachage des nœuds ouverts, il est maintenant possible d'accéder directement à la position d'un nœud dans le tableau correspondant à l'arbre binaire du tas.
-
assigneCout(noeudOuvert, cout(noeud)) : assigne simplement un nouveau coût à un nœud. Comme le nœud est ouvert, il n'a pas encore d'enfants et il n'est donc pas nécessaire de s'en préoccuper.
-
repositionneHaut(Tas, cellule) : fonction décrite dans l'Algorithme 2. Permet de repositionner, vers le haut, un nœud dans le tas en fonction de son nouveau coût, qui est plus petit que l'ancien..
-
attacheNoeud(noeudOuvert, parent(noeud)) : attache noeudOuvert au parent du nœud actuellement traité. L'objectif est de déplacer le nœud à un endroit moins profond de l'arbre de recherche et donc relatif à un moindre coût.
Dans les deux cas, une fois l'arbre de recherche modifié, la fonction retournera vrai pour signaler que le nœud est un doublon. Tout le travail pour modifier l'arbre aura déjà été effectué en amont. Le nœud courant n'a donc plus besoin d'être inséré par la suite.
6.4.3 Priorité de la liste d'attente
Le tas est organisé de façon à ce que les nœuds les plus prometteurs soient prioritaires. La méthode simple consiste à placer en tête de liste ceux pour lesquels le coût est le plus petit. Il est cependant possible d'affiner ce résultat. En cas d'égalité pour les valeurs de , une deuxième condition portant sur les valeurs de est ajoutée. Pour deux valeurs égales de , la plus petite valeur de sera prioritaire tel qu'illustré sur la Figure 6.5.
Trier le tas d'une façon différente consiste à adapter la fonction estPlusPetit(noeud1, noeud2) utilisée dans les Algorithmes 2 et 3. Cette fonction définit explicitement dans quelles conditions un nœud est plus petit, et donc possède une meilleur priorité, qu'un autre.
6.4.4 Exemple
La Figure 6.5 représente les différentes structures qui interviennent lors d'un parcours A*. Pour une lecture plus facile, la liste d'attente n'est pas représentée sous la forme d'un tas mais sous celle d'une liste chaînée triée. On voit que le parcours se dirige assez facilement vers le nœud solution 15 en évitant les autres nœuds dont le coût est plus élevé. Si aucune solution en 5 poussées n'était possible, le prochain nœud traité serait le premier de la liste d'attente et donc celui qui est le plus prometteur en 6 poussées.
6.5 Parcours IDA*
parcours IDA* : Iterative Deepening A* est entièrement basé sur l'algorithme A*. Il possède la particularité de fixer une valeur afin que tous les nœuds pour lesquels soient directement rejetés. En incrémentant la valeur de à chaque itération de l'algorithme A*, le parcours IDA* finira par trouver la solution optimale.
6.5.1 Fonctionnement
Le parcours IDA* fonctionne sur base d'itérations successives du parcours A* pour lesquelles la valeur de est fixée dès le départ. Ainsi, nous pouvons imaginer que la première itération s'effectuera avec , la deuxième avec et ainsi de suite. Chaque itération va tester toutes les possibilités dont les coûts seront dans la limite précisée. Si aucun nœud solution n'est trouvé, le coût maximal sera incrémenté et le parcours A* sera relancé jusqu'à l'obtention d'une solution.
Cette façon de procéder permet aux différentes itérations du parcours A* de supprimer rapidement de l'arbre de recherche, les sous-arbres dont il sait déjà que les solutions potentielles ne se trouvent pas dans la limite précisée. Prenons par exemple le cas où . À un endroit donné de l'arbre de recherche, nous obtenons un nœud pour lequel , et donc . Nous pouvons rejeter ce nœud et par la même occasion tous ses enfants car, au mieux, la solution que l'on y trouvera s'effectuera en 11 poussées. Nous avons donc évité un parcours inutile seulement après les deux premières poussées.
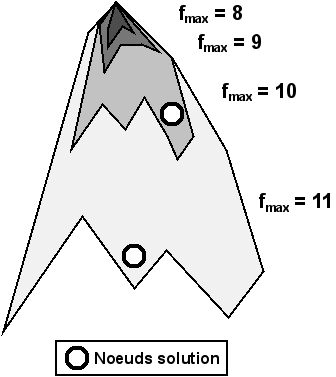
La Figure 6.6 montre différentes itérations du parcours A*. Nous pouvons y voir que la solution optimale sera toujours trouvée la première (lors de l'itération pour laquelle ). Des solutions moins bonnes pourraient être trouvées lors d'itérations suivantes.
6.5.2 Avantages
-
La solution optimale sera trouvée avec un arbre de recherche plus petit et donc avec une utilisation moins importante de la mémoire. Cela est dû à la suppression de tous les nœuds pour lesquels le coût est plus grand que l'objectif visé.
- À la fin d'une itération du parcours A* pour laquelle , il y a deux possibilités :
6.5.3 Inconvénients
L'inconvénient principal de ce parcours est qu'une même partie de l'arbre de recherche sera explorée plusieurs fois lors d'itérations successives du parcours A*. Ce n'est pas un problème majeur car, dans un arbre, la variation du nombre de nœuds d'une itération à une autre est souvent exponentielle. La dernière itération a donc, la plupart du temps, la propriété d'englober toutes les itérations précédentes en terme de temps de calcul.
6.5.4 Optimisations
Deux optimisations ont été mises en place afin d'éviter d'incrémenter le coût en partant de 1 et uniquement par pas de 1.
Valeur initiale de
L'état initial d'un problème possède un coût qui lui est propre. Il est inutile de commencer à appliquer le parcours A* sur cet état avec une limite plus basse que son coût. En effet, le premier nœud rencontré serait directement rejeté. La limite initiale à appliquer est donc le coût de l'état initial.
Incrémentation de
Nous avons remarqué que l'évolution du coût a tendance à évoluer par pas de 2. En effet, si le pousseur est placé du mauvais côté pour pousser une caisse, il va d'abord devoir la pousser une première fois, la contourner, puis la repousser une deuxième fois (cf. Figure 6.7). L'estimation du coût est ainsi faussée de 2 poussées. Pour ne pas inutilement incrémenter la limite par pas de 1 si on peut progresser plus rapidement, nous allons garder en mémoire le nœud rejeté dont le coût est le plus petit. Par exemple si la limite actuelle est de 10 et qu'à la fin de l'itération, le coût le plus petit qui a été rejeté est 12, nous pourrons commencer l'itération suivante à 12.
6.5.5 Priorité de la liste d'attente
Avec le parcours IDA* et contrairement au parcours A*, il est possible de trier la liste d'attente des nœuds uniquement par rapport à la valeur de . En effet, étant donné que la valeur de est majorée par , la seule contrainte de priorité concerne le nombre de poussées restantes pour qu'un nœud mène à une solution.
Trier le tas d'une façon différente consiste à adapter la fonction estPlusPetit(noeud1, noeud2) utilisée dans les Algorithmes 2 et 3. Cette fonction définit explicitement dans quelles conditions un nœud est plus petit, et donc possède une meilleur priorité, qu'un autre.
Chapitre 7 Estimation
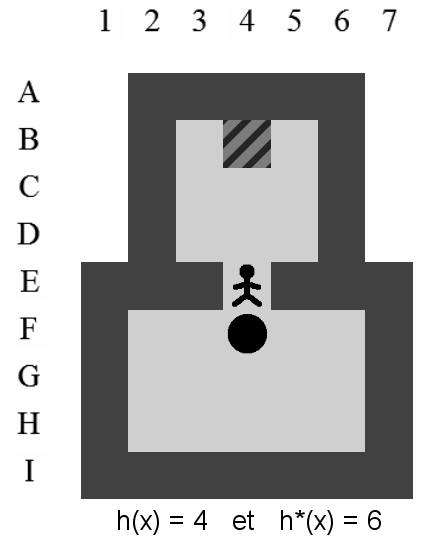
Nous avons vu dans le cadre du parcours A*, et par extension IDA*, que l'efficacité du parcours dépendait de la précision de l'estimation de où est un nœud de l'arbre de recherche. Estimer correctement le nombre de poussées restantes pour trouver une solution à partir d'un état de l'arbre de recherche est une opération très difficile. Le plus dur est certainement de ne jamais surestimer la valeur de . Si, lors de la résolution, , le parcours A* ne garantit plus l'obtention de la solution optimale.
Le parcours A* peut aboutir à une solution optimale avec une estimation peu précise. Cependant, ce n'est qu'avec une très bonne estimation qu'il montre sa réelle efficacité. Il est bon de se rappeler que si , c'est-à-dire si l'estimation est parfaite, le parcours dans l'arbre de recherche irait directement de la racine vers la solution.
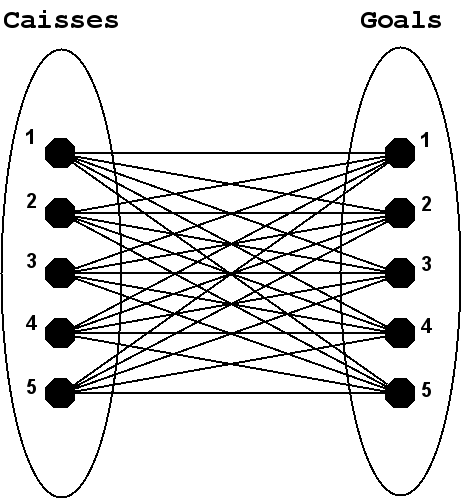
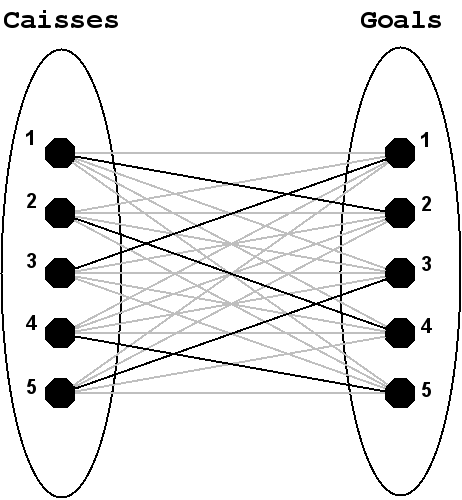
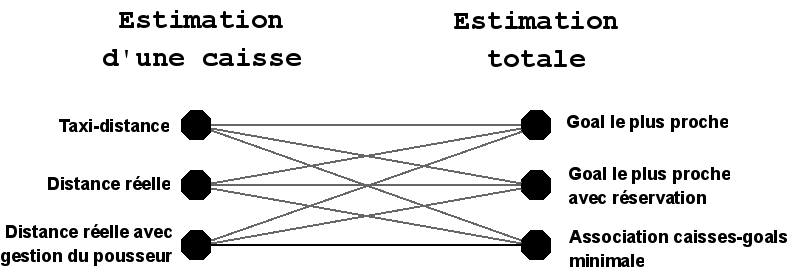
Pour trouver la valeur de , l'idée principale est d'estimer le nombre de poussées nécessaires pour placer chaque caisse de l'état sur un goal. Le problème doit alors être décomposé en deux parties.
- Calculer le plus précisément possible le nombre de poussées requises pour placer une caisse sur chacun des goals. Nous appellerons cela l' estimation d'une caisse.
- Diriger les caisses présentes dans un état vers les goals de manière à trouver l' estimation totale de l'état la plus juste possible. Il faut s'aider des estimations des caisses et il est important de continuer à minorer .
7.1 Estimation d'une caisse
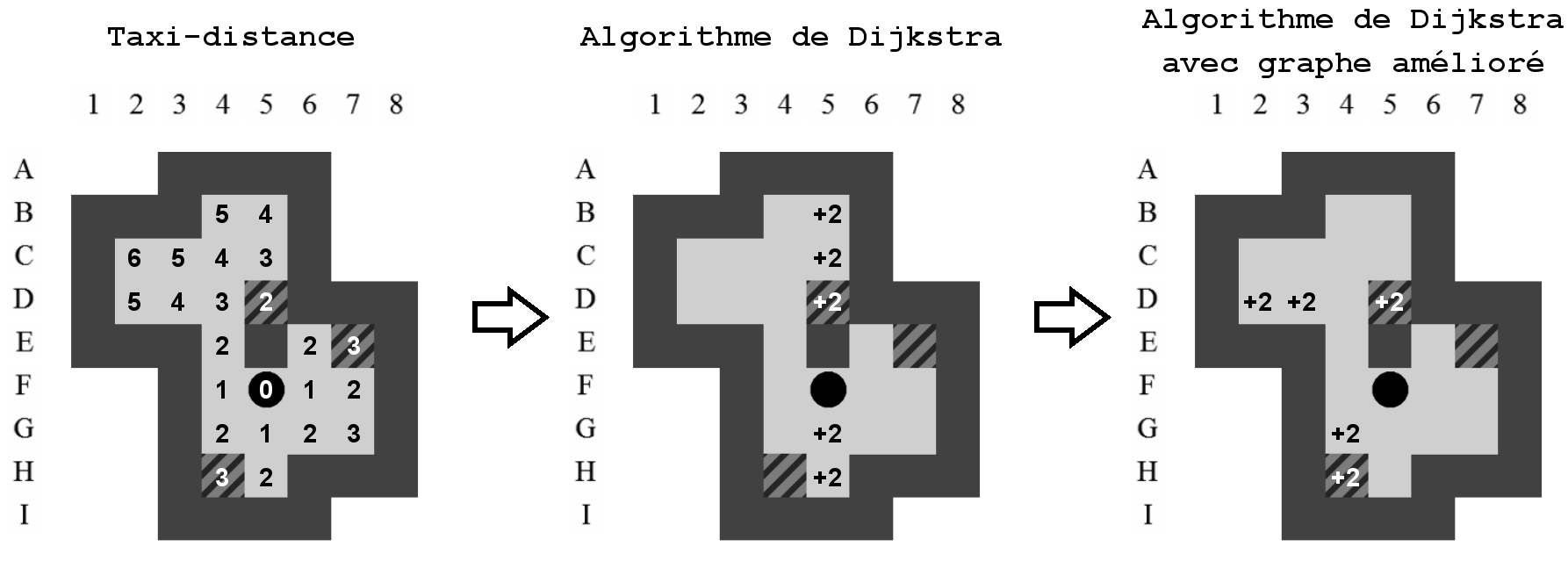
Il y a différentes façons de calculer l'estimation d'une caisse. Plus l'estimation sera précise et plus la taille de l'arbre de recherche aura tendance à diminuer. La méthode la plus simple, la taxi-distance est de loin la plus approximative. La méthode la plus précise, qui prend en compte les positions successives du pousseur, est aussi la plus coûteuse et demande l'application d'un algorithme assez lourd basé sur celui de Dijkstra.
Comme nous le verrons dans le Chapitre 10, le temps de calcul de l'estimation des caisses n'est pas un problème majeur. Ceci est lié au fait que le calcul n'est réalisé qu'une seule fois par niveau. Par la suite, les résultats seront réutilisables à l'infini. Il est donc préférable d'utiliser les méthodes les plus précises même si elles s'avèrent souvent plus lentes.
Chaque état contient des caisses sur des emplacements différents. Celles-ci peuvent potentiellement occuper toutes les positions internes d'un niveau (cf. Figure 5.3). Nous allons construire une matrice carrée , où est le nombre de positions internes, et dans laquelle la cellule où contiendra le nombre de poussées requises pour déplacer une caisse située sur la position vers la position . Cette matrice sera aussi appelée la table des estimations.
En théorie, nous n'avons besoin que des estimations des caisses vers les différents goals. Dans la pratique il est intéressant de généraliser pour trouver les estimations des caisses vers toutes les positions. Ces informations nous seront utiles dans la suite pour, par exemple, le calcul des macro-poussées (cf. Section 12.1). De plus, avec l'algorithme de Dijkstra, connaître les estimations des caisses vers les goals ou vers l'ensemble des autres positions nécessite, à peu de choses près, la même quantité de calculs.
7.1.1 Taxi-distance
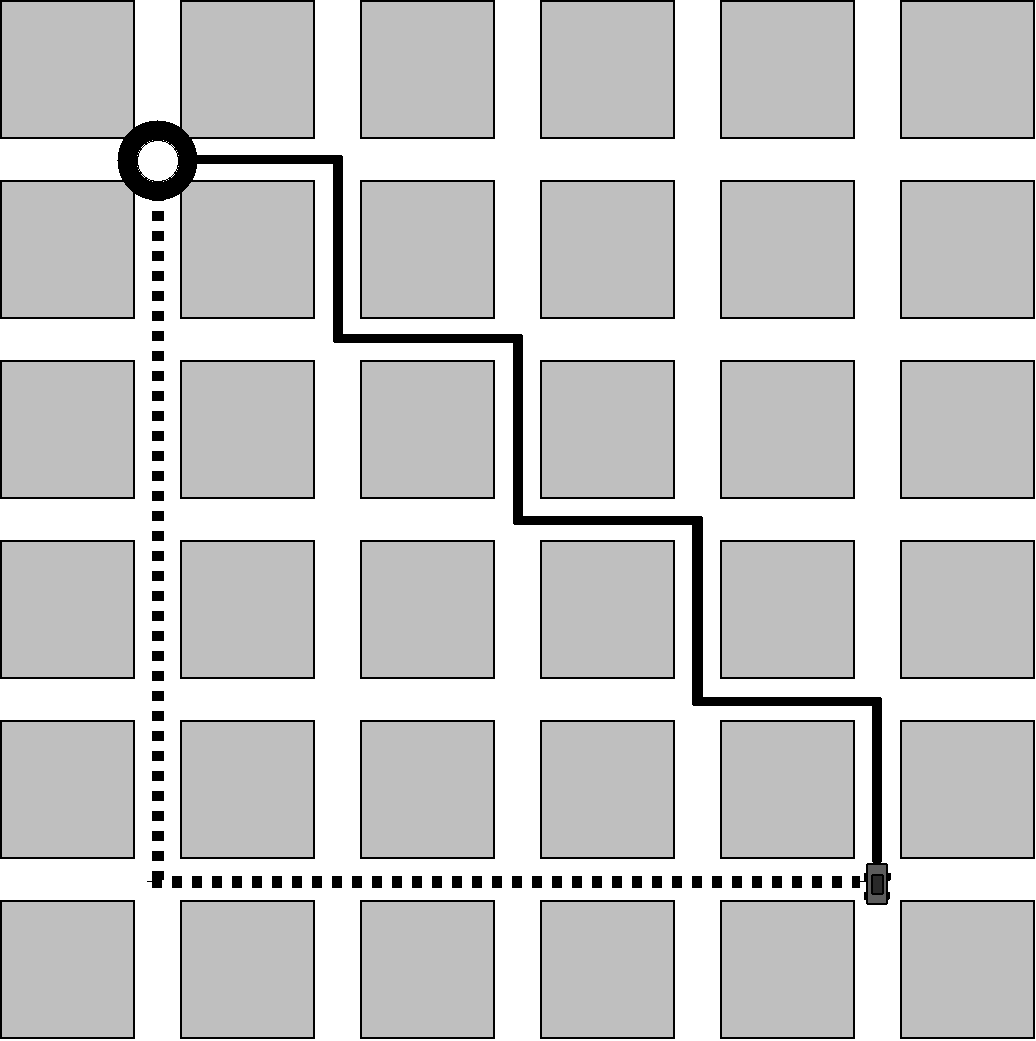
La taxi-distance, aussi appelée Distance de Manhattan, doit son nom à la distance que doivent effectuer les taxis de Manhattan pour joindre deux points dans la ville. Étant donné la structure de Manhattan qui est composée de quartiers rectangulaires et alignés, la distance réellement parcourue par un taxi correspondra à notre définition et non à la distance euclidienne. La Figure 7.1 montre que, quel que soit le chemin emprunté par le taxi dans Manhattan, la longueur totale vaudra 8 longueurs de blocs et correspondra à la taxi-distance.
Les déplacements du pousseur et des caisses, dans le jeu de Sokoban s'apparentent aux déplacements d'un taxi new-yorkais. La taxi-distance est donc une méthode simple s'appliquant au Sokoban pour mesurer la distance entre deux points de l'aire de jeu.
La Figure 7.2 représente la taxi-distance entre la caisse se situant sur la position F5 et l'ensemble des autres positions joignables.
Comme la taxi-distance représente le chemin le plus court entre un point et un point si aucun obstacle n'est dans le chemin, il parait clair que cette estimation conservera toujours la propriété d'admissibilité du parcours A*. Les obstacles (caisses et murs) qui pourraient gêner le déplacement de la caisse ne pourraient qu'augmenter la valeur obtenue par la taxi-distance.
7.1.2 Distance réelle
La distance réelle représente la distance obtenue pour mettre une caisse sur un goal à l'aide de l'application de l'algorithme de Dijkstra .
Un niveau de Sokoban peut toujours être transformé en graphe connexe. Celui-ci sera utilisé pour appliquer l'algorithme de Dijkstra sur les caisses et trouver les distances les plus courtes entre celles-ci et les goals.
Le graphe connexe créé correspond aux déplacements possibles des caisses. Soit et , trois positions alignées dans un niveau, les conditions requises pour qu'une caisse située en puisse bouger en sont les suivantes :
- La position ne doit être ni un mur, ni une caisse. Elle correspond à l'emplacement du pousseur avant la poussée.
-
La position ne doit être ni un mur, ni une caisse. Elle correspond à l'emplacement de la caisse après la poussée.
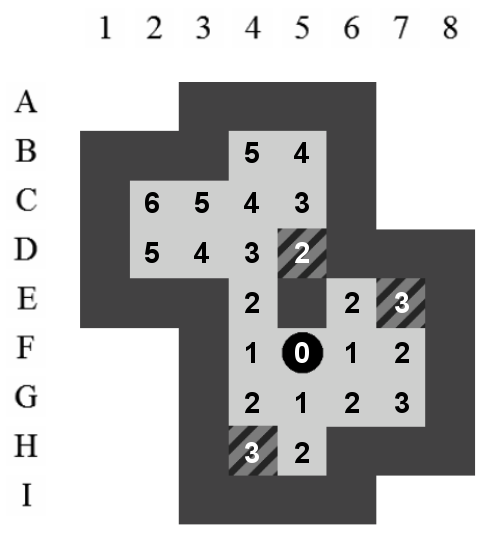
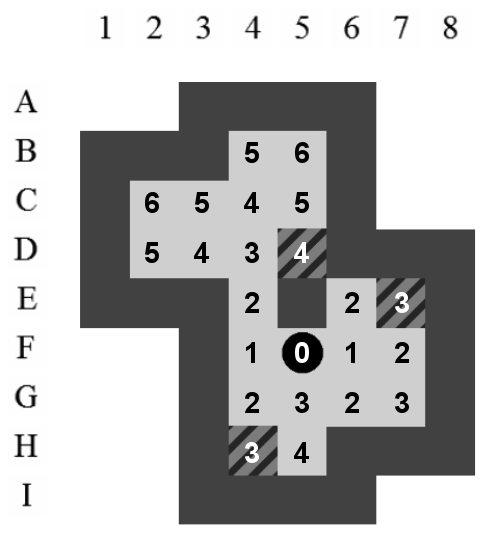
La Figure 7.3 représente le graphe connexe utilisé pour calculer l'estimation de la caisse F5 ainsi que le niveau qui comprend les estimations obtenues de la sorte. Sachant que chaque arc du graphe possède un poids unitaire, il est facile d'y appliquer directement l'algorithme de Dijkstra. L'objectif est de trouver le chemin minimal permettant de pousser la caisse vers les trois goals et , et par la même occasion, les chemins minimaux de la caisse vers toutes les autres positions.
En comparant l'estimation obtenue par l'algorithme de Dijkstra avec celle obtenue par la taxi-distance, on peut déjà remarquer une augmentation des valeurs de certaines positions. L'estimation pour joindre le goal situé sur la position D5 passe de 2 à 4. La propriété d'admissibilité est conservée car, en aucun cas, un chemin plus court que celui de l'algorithme de Dijkstra ne pourra être trouvé.
7.1.3 Distance réelle avec gestion du pousseur
Dans la section précédente, la méthode que nous avons utilisée pour construire le graphe connexe possède un défaut majeur : elle ne prend pas en compte la position du pousseur lors des déplacements successifs des caisses. Ce manquement peut mener à négliger une partie des poussées nécessaires pour positionner une caisse sur un goal.
À titre d'exemple, sur la Figure 7.3, après une poussée de E4 vers D4, le pousseur se trouvera sur la position E4. Par la suite, il n'aura pas la possibilité de déplacer la caisse sur la position D5, contrairement à ce qui est indiqué dans le graphe.
Deux solutions sont envisageables pour calculer les estimations des caisses en prenant en compte les positions successives du pousseur : l'application d'un parcours en largeur et la création améliorée du graphe connexe.
Parcours en largeur
Dans le but de réutiliser des fonctionnalités qui ont déjà été implémentées, cette méthode passe par la création d'un niveau temporaire comprenant une seule caisse et un seul goal. Sur ce niveau, un parcours en largeur sera appliqué tel qu'il a été décrit dans la Section 6.1. Celui-ci permet de trouver la solution optimale d'un niveau. Le nombre de poussées de la solution optimale servira donc d'estimation pour déplacer une caisse de la position vers la position .
Cette méthode peut rapidement être mise en place à partir du parcours en largeur déjà existant. La complexité pourrait néanmoins poser un problème.
-
Le parcours en largeur est de complexité où est le facteur de branchement et la profondeur de l'arbre de recherche. Notons que la profondeur de l'arbre dépend indirectement de , le nombre de positions internes du niveau.
-
Il faut appliquer parcours en largeur pour calculer l'entièreté de la matrice , où est le nombre de positions internes.
La quantité de calculs va exploser pour certains niveaux qui possèdent plusieurs centaines de positions. Même si cette situation se présente peu dans nos 90 niveaux de test, il vaut mieux trouver une méthode moins coûteuse afin de pouvoir l'utiliser dans un plus grand nombre de cas.
Création améliorée du graphe connexe
Tout en conservant l'utilisation de l'algorithme de Dijkstra, nous créons un graphe connexe en y intégrant l'information de la position du pousseur. Pour atteindre cet objectif, la première chose à faire est de multiplier les sommets dans le graphe. Chaque position interne du niveau est représentée par, au maximum, quatre sommets.
- : la caisse se situe sur la position et vient de droite.
- : la caisse se situe sur la position et vient de gauche.
- : la caisse se situe sur la position et vient du haut.
-
: la caisse se situe sur la position et vient du bas.
Implicitement, la provenance de la caisse indique la position du pousseur. Celui-ci se situe sur l'emplacement précédent de la caisse et possède une certaine liberté de mouvements (la zone du pousseur). Lorsqu'il est impossible pour une caisse de joindre une position par une certaine direction, le sommet correspondant à cette direction n'est pas utilisé dans le graphe.
Un arc , où et sont deux sommets du graphe connexe, signifie que “Si la caisse est venue par la droite sur la position i, alors le pousseur est capable de pousser la caisse vers le bas sur la position j”.
Les arcs dans le graphe relient toujours deux sommets qui correspondent à des positions voisines. Deux sommets qui correspondent à la même position ou à des positions non voisines ne sont donc jamais reliés entre eux.
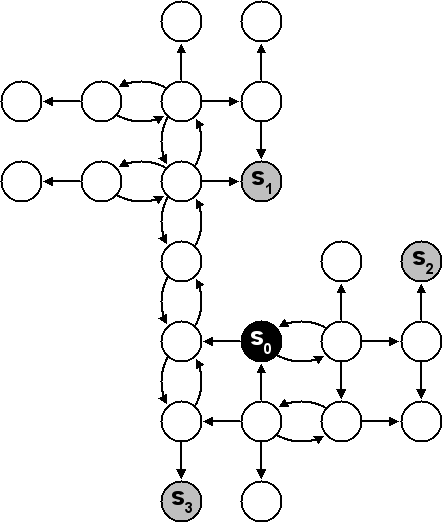
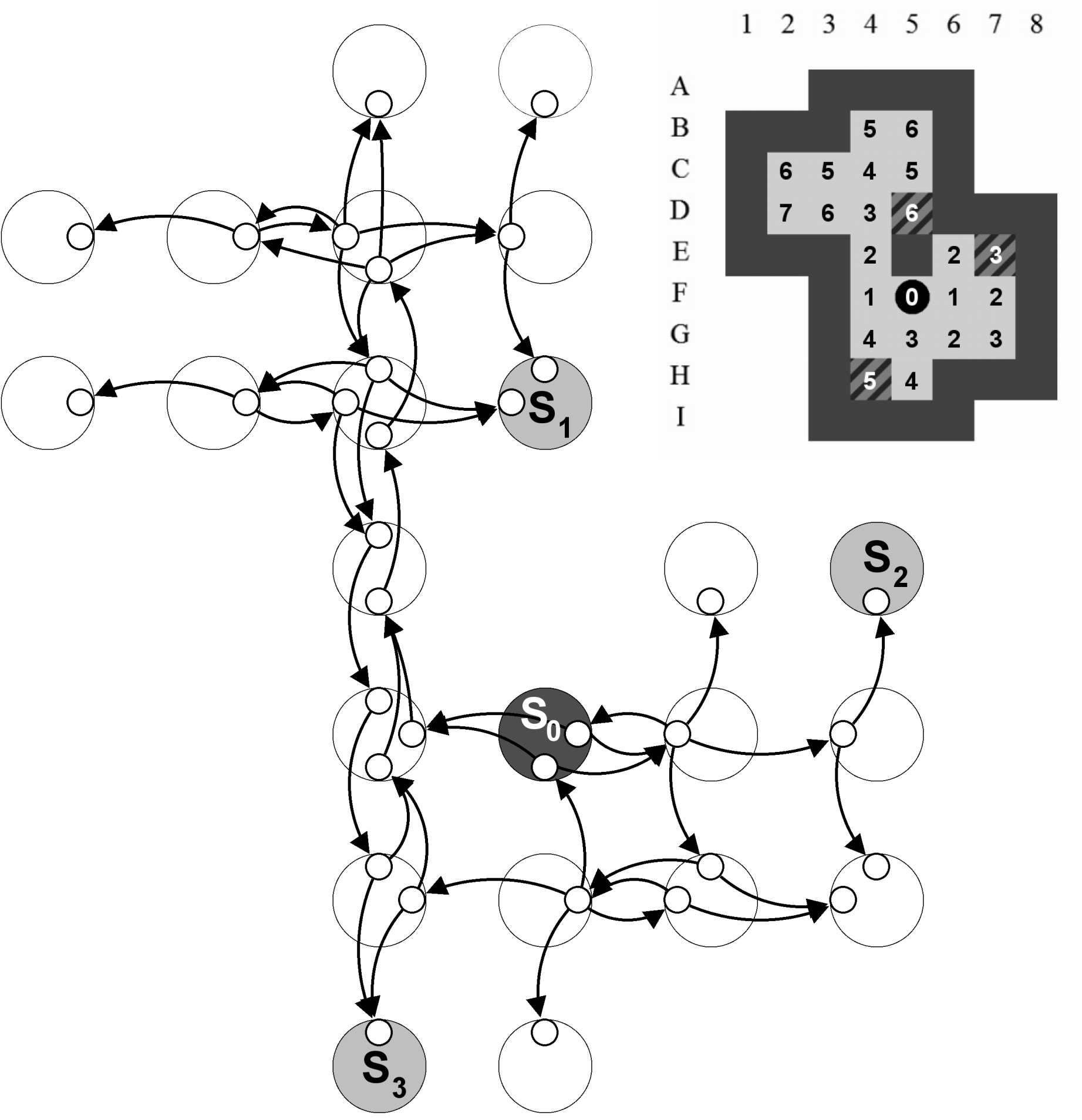
La Figure 7.4 représente le graphe connexe amélioré obtenu en procédant comme indiqué. Pour une meilleure lisibilité, les sommets qui correspondent à une même position sont entourés par des cercles plus clairs. Ceux-ci ne sont pas à prendre en considération dans le graphe connexe. Même si le graphe connexe semble peu lisible à première vue, il est possible de transiter d'un sommet à l'autre en partant de pour arriver à l'un des goals. L'important est de remarquer que le chemin emprunté sera plus long que sur la Figure 7.3 car les contraintes imposées par la position du pousseur ne permettent pas toujours le déplacement voulu.
Lorsque plusieurs sommets représentent une position de départ, l'algorithme de Dijkstra est appliqué sur chacun de ces sommets et la plus petite valeur obtenue est conservée. Ceci afin d'éviter une surestimation éventuelle de la valeur de dans des cas particuliers. Lorsque plusieurs sommets représentent une position d'arrivée, celui qui possède la valeur la plus petite sera conservé.
Implémentation
La construction du graphe se fait à l'aide de quatre tableaux et . Chaque case de ces tableaux correspond à une position dans le niveau. Chaque tableau correspond à l'un des 4 sommets de la position. représentera donc le sommet de notre graphe. L'algorithme de Dijkstra est adapté à cette structure particulière. Lorsque l'algorithme a terminé de s'exécuter sur les 4 tableaux, il suffit de récupérer la valeur pour obtenir l'estimation de la caisse vers la position .
Complexité
L'algorithme de Dijkstra s'appuie sur l'utilisation d'une liste des sommets à traiter. Dans notre cas, il s'applique toujours sur des graphes connexes dont les arcs ont des poids unitaires. L'utilisation d'une file permet donc de toujours conserver le sommet de poids le plus faible en tête de liste. Avec une fonction d'extraction en complexité , la complexité de l'algorithme est en où représente le nombre de sommets et représente le nombre d'arcs. Sachant qu'il y a, au plus, sommets et arcs, où est le nombre de positions internes du niveau, la complexité peut s'écrire . La complexité de l'algorithme de Dijkstra est donc linéaire sur le nombre de positions internes au niveau.
Le parcours en largeur proposait de remplir l'entièreté de la matrice en parcours. La solution basée sur Dijkstra permet de la remplir en seulement itérations de l'algorithme. En effet, l'algorithme de Dijkstra permet de calculer les estimations de toutes les positions à partir d'une position de départ, contrairement au parcours en largeur qui ne permettait de calculer l'estimation de la caisse que vers une seule position à la fois. Il est donc possible de remplir une ligne de la matrice en une seule itération de Dijkstra.
Conclusion
-
Le parcours en largeur propose de calculer les estimations de toutes les positions internes à l'aide de itérations d'un algorithme en où , la profondeur de l'arbre de recherche, dépend indirectement de . La solution propose donc un temps exponentiel.
-
L'algorithme de Dijkstra, appliqué sur un graphe connexe amélioré, permet de calculer les estimations de toutes les positions internes avec itérations de l'algorithme qui est en . La solution propose donc une complexité quadratique .
Comme les deux solutions permettent de compléter la matrice avec les mêmes valeurs, il est préférable d'utiliser l'algorithme de Dijkstra qui possède une complexité moindre.
7.2 Estimation totale
L'estimation totale consiste à additionner intelligemment les estimations des caisses vers les goals pour trouver la valeur de la plus juste possible, tout en continuant à minorer .
La section précédente permet de construire une matrice de taille dans laquelle une case , où , contient le nombre de poussées requises pour déplacer une caisse située sur la position vers la position .
Pour trouver la valeur de où est un nœud de l'arbre de recherche, il faut commencer par récupérer un sous-ensemble de la matrice correspondant aux positions des caisses et des goals présents dans le nœud actuel. L'objectif est donc de construire une matrice de taille où est le nombre de caisses et est le nombre de goals avec . La case , où et , contient le nombre de poussées requises pour déplacer la caisse vers le goal.
La Figure 7.5 représente un nœud ainsi que la matrice correspondante. Pour être fidèle à la réalité, la matrice utilisée pour créer la matrice a été générée à l'aide de la méthode de la Section 7.1.3 impliquant Dijkstra et le graphe amélioré. L'intersection entre la ligne et la colonne contient l'estimation requise pour positionner la caisse sur le goal .
Il est possible que certaines intersections contiennent la valeur . C'est le cas lorsqu'une caisse ne peut pas atteindre un certain goal car elle se situe sur une position particulière comme un bord ou un coin. Par exemple, sur notre niveau de test, si une caisse se trouvait sur la position F8, elle ne pourrait se diriger que vers . Ses estimations pour joindre les autres goals et seraient assignées à .
L'objectif de cette section consiste à trouver une association caisses-goals permettant de maximiser l'estimation totale. La difficulté réside dans le fait qu'il faut continuer à borner inférieurement pour que la valeur soit admissible.
7.2.1 Goal le plus proche
La solution la plus simple, mais également la moins efficace, consiste à associer chaque caisse à son goal le plus proche. Dans notre exemple, cela conduit à associer avec , avec et avec pour un total de .
Il est à souligner que, dans cette solution, deux caisses ont pour destination le même goal, ce qui s'avère impossible dans la pratique. Cette façon de procéder conserve la propriété d'admissibilité car les caisses se dirigent toujours vers le goal le plus proche, ce qui ne peut que minimiser ou égaler la valeur de .
7.2.2 Goal le plus proche avec réservation
Cette méthode améliore la précédente et permet d'éviter l'utilisation indésirable d'un même goal par plusieurs caisses. Elle permet de bloquer un goal lorsque celui-ci devient, pour la première fois, la destination de l'une des caisses. Les caisses restantes ont alors moins de possibilités de déplacements.
Ce qui nous mène à un total de . Le problème de cette méthode est que le goal associé à la dernière caisse lui est imposé. Avec parfois une estimation excessive.
Cette méthode ne conserve pas la propriété d'admissibilité car il existe des états pour lesquels . L'un de ces états est illustré sur la Figure 7.6. Dans celui-ci, et . Ceci est dû au fait que, pour minimiser l'estimation totale, il est plus intéressant de déplacer la caisse vers le goal le plus éloigné () que vers le goal le plus proche ().
7.2.3 Association caisses-goals minimisant l'estimation totale
Pour que la méthode puisse donner des résultats admissibles, il faut qu'elle soit capable de trouver une association entre les caisses et les goals, à l'aide de la matrice , de manière à minimiser l'estimation totale. La matrice , qui contient les estimations des caisses vers chacun des goals, peut être représentée dans un graphe biparti tel qu'illustré sur la Figure 7.7. Chaque arête du graphe biparti possède un poids. L'arête qui relie la caisse au goal possède le poids relatif à la position de la matrice.
Remarquons que nous obtenons là un problème typique d'assignation dans un graphe biparti complet pondéré. Le but est de trouver la couverture de poids minimum (minimum weighted bipartite matching) permettant de pousser chaque caisse sur son goal. Pour cette opération, un algorithme se présente à nous : la méthode Hongroise. Gardons à l'esprit que cet algorithme est en où représente le nombre de caissesFrank (Pas d'année). La puissance demandée pour ce traitement, à chaque nœud de l'arbre de recherche, représente une partie très gourmante de notre solveur.
Implémentation
Pour ne pas devoir réimplémenter la méthode Hongroise à partir de rien, une version C++ existanteWeaver (Pas d'année), déjà déboguée et optimisée, a été intégrée à notre solveur. Nos données ont été adaptées pour correspondre aux contraintes des fonctions existantes.
7.3 Méthodes utilisées
Trois méthodes ont été présentées pour calculer l'estimation d'une caisse et trois méthodes ont été présentées pour calculer l'estimation totale. En théorie il y a donc neuf possibilités d'associations entre ces méthodes comme illustré sur la Figure 7.8. Dans la pratique, on peut directement éliminer la méthode de la Section 7.2.2 du goal le plus proche avec réservation car elle ne respecte pas la propriété d'admissibilité du parcours A*. Si une solution est trouvée, il ne sera donc pas possible d'affirmer que celle-ci est optimale.
Des six associations restantes possibles et qui sont admissibles, il est préférable de prendre celle qui maximise l'estimation de manière à être le plus proche de la valeur . Comme le démontre la Figure 7.9, c'est l'algorithme de Dijkstra avec graphe amélioré qui majore le plus l'estimation d'une caisse vers chacune des positions. C'est donc la méthode qui s'avère la plus efficace. Rien d'étonnant à cela, c'est la méthode qui prend en compte le plus de contraintes, dont la position du pousseur.
La méthode Hongroise, qui permet de trouver l'association entre les caisses et les goals qui minimise l'estimation totale, s'avère la plus coûteuse. Elle possède une complexité en où est le nombre de caisses. Les estimations totales qu'elle obtient sont cependant nettement plus précises que celles obtenues par la méthode des goals les plus proches.
Pour calculer , nous allons donc trouver les estimations de chacune des positions (la matrice ) par la méthode de la distance réelle avec gestion du pousseur. Ensuite, nous calculerons l'estimation totale à l'aide de l'association caisses-goals minimisant l'estimation totale.
Chapitre 8 Deadlock
De manière générale, un deadlock est provoqué par un sous-ensemble des caisses de l'état qui provoque une situation dans laquelle il est impossible de pousser toutes les caisses sur des goals.
Si nous parcourons l'arbre de recherche en ignorant ces deadlocks, il est fort probable que nous obtenions un nombre très conséquent de sous-arbres condamnés à ne jamais aboutir à une solution. La taille de l'arbre va alors augmenter de manière importante. C'est pourquoi il existe plusieurs procédés afin d'éviter ce problème.
8.1 Deadlock à une caisse
Le deadlock à une caisse est celui qui se produit le plus fréquemment. Il correspond à un cas particulier de deadlock provoqué par un sous-ensemble de caisses de l'état qui ne comprend qu'une seule caisse. Ceux-ci sont répartis en deux catégories : deadlocks en coin et deadlocks en ligne.
8.1.1 Deadlock en coin
Un exemple de deadlock en coin est illustré sur la Figure 8.2. Selon les règles du jeu, il parait clair que la caisse située sur la position absolue D2 ne pourra pas rejoindre l'un des goals.
Pour détecter les positions qui provoquent des deadlocks en coin, nous parcourons toutes les positions internes d'un niveau afin de tester si elles sont bornées par des murs, sur deux côtés consécutifs, de manière à former un coin. Si tel est le cas, nous enregistrons une zone ne comprenant que les positions concernées comme illustré à l'aide de croix sur la Figure 8.2. La zone sera utilisée par la suite afin de rejeter de l'arbre de recherche tous les états qui ont une caisse sur l'une des croix.
8.1.2 Deadlock en ligne
Un exemple de deadlock en ligne est illustré sur la Figure 8.3. Selon les règles du jeu, il parait clair que la caisse située sur la position absolue C2 ne pourra pas s'écarter du mur pour rejoindre l'un des goals.
Les deadlocks en ligne sont provoqués par des murs qui ne possèdent pas de possibilité d'échappement, c'est-à-dire un passage par lequel le pousseur pourrait repousser la caisse dans l'autre sens. La méthode utilisée pour détecter les lignes problématiques consiste à utiliser les positions de deadlock en coin. En se servant de l'une de ces positions pour en joindre un deuxième via une ligne droite, si l'un des deux côtés de cette ligne droite est exclusivement formé de murs, alors nous pouvons considérer toutes les positions de cette ligne comme des deadlocks.
Une fois tous les deadlocks en ligne trouvés, nous enregistrons une zone ne comprenant que les positions concernées comme illustré à l'aide de croix sur la Figure 8.4. La zone sera utilisée par la suite afin de rejeter de l'arbre de recherche tous les états qui ont une caisse sur l'une des croix.
8.1.3 Implémentation
Grâce à l'utilisation des zones, les deadlocks à une caisse sont rapidement évincés de l'arbre de recherche. L'idée consiste à créer une zone comprenant toutes les positions pour lesquelles l'état sera déclaré comme un deadlock si une caisse s'y trouve. Une telle zone est illustrée sur la Figure 8.5.
Posons la zone des caisses d'un état . La méthode consiste à tester, pour chaque nouvel état rencontré lors du parcours de l'arbre de recherche, l'affirmation . Si l'affirmation est vraie, alors l'état ne possède pas de deadlock à une caisse. Si l'affirmation est fausse, cela signifie qu'une caisse de l'état en cours se situe sur une position de deadlock et l'état est alors rejeté.
8.2 Deadlock à plusieurs caisses
Le deadlock à plusieurs caisses correspond à un cas particulier de deadlock provoqué par un sous-ensemble de caisses de l'état qui comprend plusieurs caisses. Ce type de deadlock est réparti en plusieurs catégories en fonction de la technique utilisée pour la détection.
8.2.1 Dernière poussée
Un type de deadlock à plusieurs caisses facile à détecter est celui induit par la dernière poussée. Il existe des situations dans lesquelles des caisses se gênent mutuellement de manière à ce qu'aucune d'entre elles ne puisse plus bouger. La méthode la plus simple pour détecter ces situations est de tester la nouvelle position de la dernière caisse poussée.
Deadlock en carré
Comme il est impossible pour le pousseur de pousser une caisse si la position derrière celle-ci n'est pas libre, un deadlock en carré provoque une situation dans laquelle aucune des caisses du carré ne pourra être dégagée. À moins que les caisses présentes dans le carré ne soient toutes sur des goals, l'état courant sera alors un deadlock et rejeté de l'arbre de recherche.
La caisse qui vient d'être poussée sur la position absolue H9 de la Figure 8.6 provoque un deadlock en carré avec les trois autres positions G8, G9 et H8.
Deadlock en Z
Le deadlock en Z est décliné en 4 versions qui sont représentées sur la Figure 8.7.
8.2.2 Deadlock Zone
La méthode de la deadlock zone a été conçue en regardant le solveur s'exécuter sur certains niveaux. Il apparaissait régulièrement que certaines caisses n'évoluaient plus dans l'un des sous-arbres de l'arbre de recherche, alors que toutes les autres caisses continuaient de bouger. En analysant la situation, le phénomène était compréhensible car, peu importe la façon dont il aurait été possible de pousser l'une des caisses bloquées, elle introduisait toujours un deadlock. L'état courant n'était donc pas reconnu comme un deadlock mais il n'était pas possible de dégager l'une des caisses bloquées sans en provoquer un. La Figure 8.8 montre cette situation par les deux caisses bloquées situées sur les positions absolues C3 et D3. Il n'est pas possible de bouger l'une de ces caisses sans provoquer de deadlock en coin.
La méthode proposée a donc pour objectif de découvrir les sous-ensembles de caisses qui ne provoquent pas directement de deadlock mais qui ne peuvent pas être poussées sans en provoquer un. De manière générale, les caisses qui sont bloquées entourent, avec des murs, un certain nombre de positions vides. Le fonctionnement de la méthode consiste à détecter des positions vides dont les caisses limitrophes sont toutes bloquées. On appellera ces positions et ces caisses bloquées une deadlock zone. La Figure 8.9 indique trois de ces deadlock zones.
deadlock zone : ensemble de positions construit comme une zone du pousseur telle que définie dans la Section 5.2 mais en admettant que la construction ne débute pas de la position du pousseur mais d'une position quelconque de l'état.
De manière générale, la méthode de la deadlock zone est assez coûteuse mais permet de détecter des situations de deadlock éventuellement provoquées par un grand nombre de caisses (cf. Figure 8.10). Cette méthode vérifie, pour chaque état, que celui-ci ne contient pas une deadlock zone. Si un état en contient une, alors il est rejeté de l'arbre de recherche.
L'aspect le plus intéressant de cette méthode est qu'elle est récursive. En effet, lorsqu'on teste si une caisse est bloquée, on teste ses déplacements possibles et on regarde si ceux-ci provoquent, ou non, un deadlock. Toutes les techniques de détection de deadlock, y compris celle de la deadlock zone, sont donc à nouveau appliquées sur l'état induit par la poussée de la caisse. Cette capacité à fonctionner récursivement permet d'anticiper des situations de deadlock plusieurs poussées avant qu'elles ne se produisent (cf. Figure 8.11).
8.2.3 Deadlock méthodique
Rappelons-nous la définition d'un deadlock : “un deadlock est un état de l'arbre de recherche à partir duquel il est impossible de trouver un état solution”. Un deadlock est souvent provoqué par un sous-état de l'état testé. Il dépend donc des positions des caisses et de celle du pousseur. On peut d'ailleurs remarquer sur la Figure 8.12 qu'un deadlock ne serait pas détecté si le pousseur occupait la position D12.
sous-état : un sous-état d'un état est un état pour lequel on peut affirmer tel que nous l'avons défini dans la Section 5.5.4.
Le deadlock méthodique consiste à tester un sous-état pour voir s'il provoque, ou non, un deadlock. Cette méthode n'utilise que des outils qui sont déjà en notre possession. Elle consiste à appliquer le solveur sur ce sous-état et à observer si une solution est possible ou si l'arbre de recherche ne peut jamais aboutir à une solution. Si le sous-état ne comprend pas trop de caisses, la présence d'une solution devrait être rapidement vérifiée.
Dans le cas où le sous-état provoque un deadlock, celui-ci sera enregistré et, par la suite, tous les états de l'arbre de recherche qui le contiennent seront rejetés.
Le solveur utilisé pour tester les sous-états ne doit pas forcément être optimal. Il doit surtout être rapide car nous ne cherchons pas une solution mais simplement la présence ou l'absence d'une solution. C'est pour cela qu'une version modifiée de notre solveur, que nous appellerons goodPushes, a été utilisée. Ce solveur utilise le même principe que le parcours A* avec l'utilisation comme coût de . La différence est que cette fois-ci, est fixé à 0. Il ne prend donc en compte que la distance entre un état donné et l'état solution, ce qui a l'avantage d'aboutir très vite à un résultat qui ne sera pas forcément optimal.
L'intérêt du deadlock méthodique est qu'il sert de soutien aux autres méthodes de deadlock. En effet, il est programmé pour ne pas prendre en compte les sous-états déjà bloqués par les autres méthodes pour limiter le nombre de sous-états à stocker en mémoire.
Il existe deux méthodes pour rechercher les deadlocks : la recherche passive et la recherche active.
Recherche passive
La recherche passive consiste à créer, à partir d'un niveau, tous les états possibles de 1 caisse, 2 caisses, 3 caisses ou plus. Le solveur goodPushes est ensuite exécuté sur chacun de ces états et ceux-ci sont enregistrés lorsqu'un deadlock est détecté. Tous les états ainsi créés sont potentiellement des sous-états qui pourraient apparaître dans l'arbre de recherche.
En fonction de la taille des niveaux, il sera parfois difficile de trouver les deadlocks de 3 caisses et plus à cause du temps de calcul. La méthode reste néanmoins très intéressante car moins un sous-état contient de caisses et plus il a de chance d'être inclus dans un état de l'arbre de recherche.
Nous verrons que la recherche passive de deadlocks est un cas particulier de la recherche passive de pénalités. La Section 9.2.1 décrit plus en profondeur la technique employée pour créer les états à 1, 2 ou 3 caisses.
Recherche active
La recherche active part du principe que la recherche passive est trop générale car elle teste des sous-états sans pouvoir affirmer qu'ils seront présents dans l'arbre de recherche. La technique employée ici consiste à essayer de détecter des sous-états qui pourraient provoquer des deadlocks dans chaque état rencontré dans l'arbre de recherche.
En fonction de la limite de puissance allouée à chaque état rencontré, il est possible de créer sur mesure des sous-états de plus de 3 caisses qui sont inclus dans l'état en cours. L'effort est ainsi dirigé vers les caisses présentes, ce qui permet d'augmenter la probabilité de trouver un deadlock utile.
Comme la recherche passive, la recherche active de deadlocks est un cas particulier de la recherche active de pénalités. La Section 9.2.2 explique comment créer des sous-états à tester à partir d'un état de l'arbre de recherche.
Chapitre 9 Pénalité
Ce chapitre décrit une technique utilisée pour affiner l'estimation d'un nœud dans l'arbre de recherche. Pour rappel, plus l'estimation de la distance restante est proche de la distance réelle , plus l'arbre de recherche sera petit et plus vite une solution optimale sera trouvée.
Les techniques développées dans le Chapitre 7 permettent d'obtenir une estimation en fonction des positions des caisses et des goals dans le nœud. Rien dans ces techniques ne permet de mettre en évidence le surcoût occasionné lorsque plusieurs caisses se gênent mutuellement.
Le cas d'un sous-état contenant des caisses qui se gênent mutuellement, illustré sur la Figure 9.1, n'est pourtant pas rare. À partir des méthodes d'estimation décrites précédemment, on obtient pour ce sous-état . Dans les faits cependant, on voit directement que la caisse située sur la position absolue H9 ne pourra pas être atteinte par le pousseur sans qu'il ne commence par pousser la caisse située en H6 vers le bas. Ce mouvement supplémentaire donnera au final . La différence entre l'estimation et le coût réel est donc de 2.
Cette différence entre coût estimé et coût réel du sous-état, que nous appellerons pénalité d'un sous-état, devra s'appliquer dans tous les états dans lesquels ce sous-état est inclus. La pénalité déduite d'un état comprend l'application des pénalités (cf. Section 9.4) de tous les sous-états tels que . Contrairement à la pénalité d'un sous-état, la pénalité déduite d'un état n'est pas toujours la différence exacte entre le coût estimé et le coût réel, ce n'est qu'une meilleure approche de la valeur
9.1 Définition
À partir d'un niveau, nous allons donc essayer de trouver un maximum de sous-états qui contiennent des pénalités. Ceux-ci vont nous aider à trouver les pénalités déduites des états de l'arbre de recherche afin d'améliorer leurs estimations de .
Cette technique est une généralisation de celle des deadlocks méthodiques (cf. Section 8.2.3). En effet, un sous-état qui provoque un deadlock peut être considéré comme un sous-état dont la pénalité est infinie. L'état qui comprend ce sous-état aura alors une pénalité déduite infinie et une valeur . Le coût du nœud contenant l'état va alors provoquer son rejet de l'arbre de recherche.
L'objectif est de rechercher des pénalités de sous-états qui ne sont pas nulles et donc des sous-états pour lesquels . Plus le nombre de sous-états trouvés sera grand et plus les coûts des nœuds de l'arbre de recherche auront la possibilité d'être précis.
-
Il faut trouver les sous-états qui apporteront une pénalité parmi un nombre très important de possibilités différentes. Nous verrons dans la Section 9.2 comment rechercher efficacement.
- Il faut pouvoir affirmer que la différence entre l'estimation de la distance du sous-état et sa distance réelle s'applique bien pour positionner les caisses présentes sur tous les sous-ensembles possibles de goals. Nous verrons dans la Section 9.3 comment une pénalité trouvée doit être validée avant de pouvoir être appliquée sur un état.
9.2 Recherche
Tout comme la méthode des deadlocks méthodiques, la recherche de sous-états potentiellement pénalisés s'effectue de deux façons : passivement et activement.
Pour vérifier qu'un sous-état provoque une pénalité, nous créons un niveau contenant les caisses du sous-état ainsi que tous les goals et nous appliquons le solveur bestPushes avec une limite où est l'estimation actuelle du sous-état testé. En appliquant un solveur optimal avec une limite fixée de poussées, nous avons deux possibilités :
-
Une solution est trouvée : la limite introduite correspond à la distance exacte entre le nœud initial et le nœud solution. L'estimation actuelle du sous-état correspond donc à la distance réelle. Aucune pénalité ne doit être assignée au sous-état.
- Aucune solution n'est trouvée : la limite introduite est plus petite que la distance exacte entre l'état initial et le nœud solution. Cela signifie que l'estimation actuelle du sous-état ne correspond pas à la distance réelle. Selon le résultat de la validation (cf. Section 9.3), le sous-état va alors être pénalisé.
9.2.1 Recherche passive
La recherche passive consiste à créer, à partir d'un niveau, tous les états possibles de 1 caisse, 2 caisses, 3 caisses ou plus. Le solveur optimal bestPushes est ensuite exécuté sur chacun de ces états avec une limite où est l'estimation actuelle de l'état testé. Lorsqu'une pénalité est détectée et validée pour un état, celle-ci est alors enregistrée.
Pour tester tous les états possibles de caisses dans un niveau qui comprend positions internes, il faut faire évoluer les caisses sur les positions selon les règles suivantes :
-
Au départ, Les caisses occupent les premières positions internes du niveau.
-
Pour créer chaque nouvel état, la technique consiste à avancer d'une position la caisse qui sait encore avancer et qui est sur la position la plus grande. Si une caisse avance sur la position et que autres caisses sont sur des positions plus grandes, celles-ci seront déplacées sur les positions avant le prochain déplacement.
-
La création de tous les états de caisses s'arrête lorsque les positions sont toutes occupées par des caisses.
Lorsque tous les états de caisses ont été créés et testés, on incrémente le nombre de caisses jusqu'à la limite désirée et on recommence ces manipulations.
La zone des caisses de chaque état sera ainsi créée à partir des positions des caisses obtenues par ce procédé. Il faut ensuite chercher toutes les zones du pousseur possibles à partir de chaque zone des caisses. Pour chaque couple possible (, ) tel qu'illustré sur la Figure 9.2, un état sera créé et testé. La position du pousseur dans le niveau transmis au solveur bestPushes n'a que peu d'importance tant qu'elle se situe bien dans la zone du pousseur trouvée. Dans notre exemple, le pousseur se situe chaque fois sur la première position relative à la zone du pousseur à tester.
9.2.2 Recherche active
La recherche active part du principe que la recherche passive est trop générale car elle teste des sous-états sans pouvoir affirmer qu'ils seront présents dans l'arbre de recherche. La technique employée ici consiste à essayer de détecter des sous-états qui pourraient provoquer des pénalités dans chaque état rencontré dans l'arbre de recherche.
Il serait trop optimiste de tester dans un temps raisonnable tous les sous-états pouvant être formés à partir des caisses présentes dans l'état. Nous allons devoir utiliser des techniques pour obtenir en un temps minimum les sous-états qui ont le plus de chances de mener à des pénalités. La méthode employée s'inspire fortement de celle des Pattern Search développée par Andreas JunghannsJunghanns (1999).
Le fonctionnement consiste à utiliser la dernière caisse poussée de l'état en cours. La première chose à faire est de rechercher la pénalité du sous-état correspondant à cette unique caisse et à la position du pousseur. À partir de la solution du niveau utilisée pour chercher la pénalité, on récupère deux éléments : le chemin du pousseur et le chemin des caisses.
Ces deux chemins vont nous servir à décider quelle caisse sera la prochaine à ajouter à l'état dont on va rechercher la pénalité. Le principe est qu'on a plus de chance d'introduire une pénalité si on ajoute une caisse qui se trouve sur le chemin de la solution précédente.
-
On insère d'abord les caisses présentes dans l'état en cours et qui se trouvent sur la plus petite position du chemin des caisses.
-
Lorsque toutes les caisses de l'état qui se trouvent sur le chemin des caisses ont été ajoutées, la caisse qui se trouve sur la plus petite position du chemin du pousseur sera à son tour ajoutée.
Nous allons ainsi introduire de nouvelles caisses jusqu'à ce que l'une des trois conditions suivantes soit remplie :
- Une pénalité est trouvée et enregistrée.
- Toutes les caisses de l'état qui se trouvent sur l'un des chemins ont été ajoutées.
-
La recherche active des sous-états pénalisés d'un état est limitée par une certaine quantité de nœuds. Si cette quantité est dépassée pour un certain état, on arrête la recherche de sous-états pénalisés.
Pour illustrer cette méthode, nous avons repris l'exemple présenté dansJunghanns (1999) La Figure 9.3 correspond à une poussée. La recherche active va s'appliquer sur la caisse qui vient d'être poussée en créant plusieurs sous-états qui sont susceptibles de provoquer des pénalités comme illustré sur la Figure 9.4.
Le chemin des caisses récupéré à partir de la solution du sous-état représenté en haut à gauche de la Figure 9.4 passe par les positions absolues C6, C5, C4, C3. On ajoute donc la caisse située sur la position C5 dans le sous-état suivant. Pour le troisième sous-état représenté, on utilise le chemin du pousseur car aucune caisse ne se trouve plus sur le chemin des caisses.
Le dernier sous-état est considéré comme un deadlock et possède donc une pénalité infinie. La recherche active s'arrête pour cet état (qui sera rejeté) et le sous-état pénalisé est enregistré. Celui-ci servira à déduire les pénalités d'autres états qui pourront être rencontrés dans la suite de l'arbre de recherche.
Nous pouvons remarquer que seulement trois des quatre caisses présentes dans le dernier sous-état provoquent un deadlock. La plus petite situation provoquant la pénalité sera recherchée lors de la validation qui est détaillée dans le chapitre suivant.
9.3 Validation
La pénalité d'un sous-état doit pouvoir s'appliquer quel que soit le sous-ensemble de goals utilisé par les caisses. Si un sous-état possède une pénalité qui ne s'applique pas quel que soit le sous-ensemble de goals utilisé, cela signifie qu'il y a au moins une possibilité d'association caisses-goals pour que la pénalité provoque une majoration de .
Sur l'exemple de la Figure 9.5, on remarque que la différence entre le coût réel et le coût estimé est de 1. Une pénalité de 1 devrait donc être assignée à ce sous-état. Cependant, il existe un sous-ensemble de goals pour lequel l'estimation correspond bien au coût réel. Dans ce cas, la pénalité n'est pas validée car elle va majorer si la solution comprend les trois caisses positionnées sur les goals F14, F15 et K14.
Si est majoré pour un nœud de l'arbre, cela signifie que nous risquons de perdre l'optimalité de la solution. Pour éviter ce cas précis, chaque sous-état pénalisé doit être testé pour voir si il s'applique bien à tous les sous-ensembles de goals.
Dès que plus de trois caisses sont comprises dans un sous-état, le nombre de sous-ensembles de goals à tester risque d'être très grand. Nous ne testerons pas tous les sous-ensembles de goals mais uniquement une partie qui se veut représentative. Pour ce faire, pour valider un sous-état de 3 caisses dans un niveau qui contient 10 goals, nous allons tester les pénalités avec les sous-ensembles de goals suivants : (1,2,3), (4,5,6), (7,8,9), (8,9,10). Remarquons que le dernier sous-ensemble est en partie redondant afin de tester toutes les positions des goals.
9.3.1 Sous-état pénalisé minimum
Il peut arriver qu'un sous-état pénalisé contienne plus de caisses que nécessaire pour que la pénalité s'applique (cf. 4ème état de la Figure 9.4). Il faut donc trouver le sous-état pénalisé minimum, c'est-à-dire le sous-état qui comprend le moins de caisses tout en provoquant la même pénalité. Pour y arriver, pour chaque état de caisses qui est validé, nous allons tester les pénalités de tous les sous-états de caisses. Par récursivité, tous les sous-états qui provoquent une pénalité seront trouvés.
9.4 Application
Pour déduire la pénalité d'un état de l'arbre de recherche, nous commençons par regrouper tous les sous-états pénalisés qui sont inclus dans celui-ci. Il n'est pas possible d'appliquer directement toutes les pénalités trouvées. En effet, celles-ci sont parfois relatives aux mêmes caisses qui ne peuvent pas être réutilisées plusieurs fois. Il faut donc trouver l'ensemble des sous-états pénalisés compris dans l'état qui maximisera la pénalité déduite sans utiliser deux fois une même caisse.
La méthode utilisée consiste à classer tous les sous-états pénalisés en fonction du nombre de caisses qu'ils contiennent en utilisant une liste par nombre de caisses. Ensuite, chaque liste sera triée par ordre décroissant de pénalité pour obtenir une organisation comme celle illustrée sur la Figure 9.6.
Avant de commencer, nous créons un état temporaire qui est une copie de l'état en cours. Ensuite, à partir du classement des sous-états, on recherche la pénalité la plus haute disponible et on prend le sous-état avec le moins de caisses correspondant à celle-ci. Pour s'assurer qu'aucune caisse ne puisse être utilisée deux fois, la zone du pousseur de est réduite des caisses présentes dans le sous-état pénalisé. On continue à procéder de la sorte tant que des sous-états pénalisés sont inclus dans l'état .
Au final, nous obtiendrons la pénalité déduite de l'état grâce à tous les sous-états pénalisés qui ont pu être inclus dans celui-ci. Cette pénalité déduite s'ajoutera à l'estimation de l'état qui a été calculée à l'aide des méthodes du Chapitre 7.
Un exemple de pénalité déduite est illustré sur la Figure 9.7. Celle-ci représente la copie de l'état en cours (en haut à gauche) qui possède une estimation de 189. Chaque fois qu'une pénalité est appliquée sur l'état en cours, les caisses correspondantes sont supprimées de et d'autres pénalités qui correspondent aux caisses restantes peuvent ensuite être appliquées. Au total, la pénalité déduite de l'état est de 10+6+4=20. L'estimation de la distance restante de l'état est donc de .
Chapitre 10 Pré-traitement
Le pré-traitement d'un niveau permet de rechercher une certaine quantité d'informations sur celui-ci avant même de commencer à parcourir l'arbre de recherche. C'est une préparation du niveau qui nous aidera à aller plus vite lors de sa résolution.
Tout l'intérêt du pré-traitement est qu'il est facultatif. C'est-à-dire qu'il est tout à fait possible d'utiliser le solveur sans pré-traitement, avec un petit pré-traitement ou encore en pré-traitant le niveau pendant plusieurs jours pour être sûr de récolter un maximum d'informations utiles.
Un autre intérêt est qu'il est tout à fait possible de continuer un pré-traitement exactement là où on l'a arrêté la dernière fois. Les informations récoltées sont persistantes et peuvent être réutilisées à l'infini. Plus le temps consacré sur chaque niveau sera important et plus le parcours de l'arbre de recherche aura des chances d'être performant.
Les pré-traitements concernent deux aspects de la résolution des niveaux que nous avons déjà vus : la table des estimations et les pénalités.
10.1 Table des estimations
La table des estimations correspond à la matrice que nous avons construite lors du Chapitre 7. Celle-ci nous permet de connaître l'estimation du coût nécessaire pour pousser une caisse de la position relative vers la position relative d'un niveau.
Même si la génération de la table des estimations est relativement rapide, il est intéressant de la calculer une seule fois et de l'enregistrer. Ainsi, nous éviterons de nombreux calculs inutiles lors de prochains essais de résolution du niveau. De plus, tous les états et sous-états d'un niveau possèdent la même table des estimations, il ne sera donc pas nécessaire de la recalculer lors de l'application du solveur bestPushes sur les sous-états dont nous voulons tester la pénalité.
10.2 Pénalités
Les pénalités correspondent aux sous-états pénalisés du Chapitre 9. En général, plus le solveur connait de pénalités avant de commencer à résoudre un niveau et moins l'arbre de recherche sera grand. La recherche passive de pénalités que nous avons vue dans la Section 9.2.1 permet de détecter des pénalités avant même de construire l'arbre de recherche.
L'intérêt du pré-traitement des pénalités est que si on recherche passivement tous les sous-états pénalisés de 3 caisses et moins, l'obtention de meilleures estimations pour les nœuds de l'arbre de recherche est fort probable. Il est donc possible de lancer la résolution d'un niveau avec l'obligation de tester d'abord tous les sous-états de 3 caisses et moins.
Cette opération pourra prendre plusieurs heures mais pourra être exécutée en plusieurs fois. En effet, la position des caisses du dernier sous-état testé sera sauvegardée et il sera donc possible de reprendre la recherche là où elle a été arrêtée.
Pour les niveaux les plus difficiles et si la puissance et le temps ne sont pas un problème, rien n'empêche l'utilisateur de continuer la recherche pour 4 caisses et plus. Chaque sous-état pénalisé supplémentaire permettra peut-être de supprimer de nombreux sous-arbres de l'arbre de recherche.
Le fichier contenant les sous-états pénalisés est le même pour la recherche passive et la recherche active de pénalités. La recherche active va donc compléter les résultats obtenus par le pré-traitement lors du parcours de l'arbre de recherche.
Chapitre 11 Post-traitement
Le post-traitement d'un niveau permet d'analyser l'arbre de recherche à la fin d'un parcours qui n'a pas mené à une solution à cause d'un dépassement de la mémoire allouée ou du nombre de nœuds maximum autorisé. Analyser l'arbre de recherche permet de trouver des informations ou des indices sur ce qui peut encore être amélioré.
De nouveau, le post-traitement est facultatif, une certaine quantité d'informations va être déduite de l'arbre de recherche mais rien n'oblige l'utilisateur à les utiliser lors du redémarrage du solveur sur le niveau.
Les post-traitements concernent deux aspects de la résolution des niveaux : l'itération du parcours IDA* et les pénalités probables qui se trouvent dans l'arbre de recherche.
11.1 Itération du parcours IDA*
Nous avons vu dans la Section 6.5 que le parcours IDA* procédait à plusieurs itérations du parcours A*, avec une valeur progressive, dans le but de limiter au mieux les efforts de chaque itération. Il arrive parfois que des millions de nœuds soient nécessaires pour qu'une itération de A* se termine entièrement sans trouver de solution pour un certain . Celui-ci va alors être incrémenté pour l'itération suivante du parcours A*.
Afin d'éviter de recommencer toutes les itérations du parcours A* à chaque exécution du solveur sur un niveau, la valeur est enregistrée dans un fichier à chaque incrémentation de sa valeur. Il est ainsi possible de reprendre la résolution d'un niveau à la dernière itération rencontrée, ce qui peut faire gagner beaucoup de temps. Il sera alors possible d'affirmer : “le niveau n'a pas de solution dont le nombre de poussées est en deçà de ”.
11.2 Pénalités probables
En analysant l'arbre de recherche, il est possible de mettre en évidence certains sous-états dont une pénalité non-détectée est probable. Ce sont généralement les sous-états qui apparaissent le plus souvent dans l'arbre de recherche.
Prenons le cas extrême où un sous-état de 4 caisses provoque un deadlock, et donc une pénalité infinie qui n'est pas détectée. Dans le sous-arbre créé à partir de la dernière poussée formant le deadlock, les 4 caisses resteront immobiles alors que toutes les autres continueront de bouger. Selon nos observations, un tel sous-arbre va souvent contenir plusieurs milliers de nœuds avant d'être abandonné au profit d'un autre plus prometteur.
Tous les nœuds de ce sous-arbre contiendront 4 caisses sur les mêmes positions. Si nous pouvions détecter tous les sous-états qui sont figés dans l'arbre de recherche et tester leurs pénalités, plusieurs sous-arbres pourraient être évités. C'est ce que nous avons essayé de mettre en place à l'aide de méthodes simples.
11.2.1 Positions fréquentes
Lorsqu'un parcours est terminé sans qu'une solution ne soit trouvée, un petit algorithme récursif va parcourir tous les nœuds de l'arbre de recherche et enregistrer le nombre de caisses positionnées sur chaque position du niveau.
- Les 15 positions les plus utilisées, excepté les positions qui correspondent aux goals.
-
Les 15 positions les plus utilisées, toutes positions confondues.
Le premier classement est créé afin de ne pas tenir compte des caisses placées sur un goal qui se situe un coin. Ces positions sont peu intéressantes dans la recherche de sous-états pénalisés. Elles ne bougent pas dans un certain sous-arbre mais ne sont pas nécessairement considérées comme des indications d'une pénalité à découvrir.
Si nous ne prenons que les 15 positions les plus utilisées, c'est uniquement par compromis entre temps de calcul et nombre de sous-états pénalisés qu'il sera possible de trouver.
11.2.2 Sous-états probablement pénalisés
En utilisant les deux classements de positions obtenus dans la section précédente, nous allons créer une liste de tous les sous-états à tester de 1 à 6 caisses pour lesquels les caisses se trouvent toutes sur l'une des 15 positions. Les sous-états de 1 à 3 caisses ne seront pas recréés s'ils ont déjà été testés lors du pré-traitement.
Ces deux listes comprennent des sous-états qui ont de fortes chances d'être pénalisés. Chaque sous-état sera enregistré dans un fichier. Si rien n'est précisé lors de la prochaine exécution du solveur sur le niveau, chaque sous-état contenu dans le fichier sera testé en pré-traitement et donc, avant le nouveau parcours de l'arbre de recherche.
Chapitre 12 Optimisations
Ce chapitre présente des fonctionnalités qui ont été intégrées dans notre solveur avec pour objectif de trouver des résultats plus vite et dans un arbre de recherche plus petit. Celles-ci sont basées sur deux méthodes. La première permet de prendre des raccourcis dans l'arbre de recherche en autorisant d'autres types de transitions plus efficaces. La deuxième permet de supprimer une certaine quantité de nœuds inutiles de l'arbre de recherche.
12.1 Macro-poussées
Les macro-poussées introduisent une nouvelle couche d'abstraction au niveau des transitions possibles dans l'arbre de recherche. Notre première couche d'abstraction était d'utiliser les poussées des caisses au lieu des mouvements du pousseur. Ceci nous avait permis de réduire considérablement l'arbre de recherche en transformant la position du pousseur en une zone du pousseur.
La nouvelle couche d'abstraction que représentent les macro-poussées se montre très pratique pour prendre des raccourcis dans l'arbre de recherche. Si une caisse peut être poussée sur un goal sans qu'il ne soit nécessaire de bouger d'autres caisses, alors un nouvel état sera créé dans l'arbre avec la caisse située sur le goal et le pousseur juste à côté. Les macro-poussées interviennent en plus des poussées régulières comme illustré sur la Figure 12.1.
Pour trouver les macro-poussées qui sont réalisables à partir d'un état de l'arbre de recherche, nous appliquons l'algorithme de Dijkstra sur le graphe connexe amélioré décrit dans la Section 7.1.3. Le but est de connaître quelles positions du niveau qui contiennent un goal peuvent être atteintes par la caisse.
Dans la Section 7.1.3, le graphe connexe calculait la distance d'une caisse vers chacun des goals sans prendre en compte les autres caisses. Cette fois-ci, toutes les autres caisses devront être considérées comme des obstacles. Le graphe connexe amélioré sera donc créé à partir de l'état courant en considérant toutes les autres caisses comme si elles étaient des murs.
Contrairement à ce que l'on pourrait croire, on n'ajoute pas toutes les macro-poussées détectées dans un état. On ajoute uniquement celles qui ont l'air les plus prometteuses. Inspirée de l'ordonnancement des goals deDemaret (2007), cette méthode n'autorise que les macro-poussées des caisses vers les goals qui sont cernés, sur les 4 positions directement voisines, par le plus de caisses et de murs.
Par exemple, admettons que soit un goal dont le voisin du haut est un mur, celui de droite une caisse et les deux autres des positions vides et que soit un goal dont trois des quatre voisins sont des positions vides. On assignera un coût 2 à et un coût 1 à . Les macro-poussées autorisées seront uniquement celles qui aboutiront sur . Cette technique permet de commencer par remplir les goals des coins et évite ainsi de bloquer des goals derrière des amas de caisses infranchissables.
En utilisant la méthode des macro-poussées, l'affirmation qui disait que représentait la profondeur d'un nœud dans l'arbre de recherche n'est plus vérifiée. En effet, la valeur d'un état obtenu après macro-poussée correspondra à la somme de la valeur de son père et du nombre de poussées relatif à la macro-poussée.
Une autre difficulté relative à l'introduction des macro-poussées concerne la remontée dans l'arbre de recherche à partir du nœud solution. Cette remontée permet de trouver le chemin emprunté par le pousseur entre le nœud initial et le nœud solution. Trouver les mouvements successifs du pousseur alors que deux couches d'abstractions sont utilisées n'est pas évident. De nombreuses techniques impliquant l'algorithme de Dijkstra au niveau du pousseur et au niveau des caisses seront utilisées.
12.2 Élagage
Nous partons de la constatation suivante : un nœud de l'arbre de recherche qui n'est pas solution et dont tous les fils sont rejetés pour cause de deadlock, coût excessif ou duplication est inutile. Ce nœud correspond à une feuille de l'arbre dont on peut affirmer qu'elle ne donnera pas naissance à un sous-arbre car aucun de ses fils n'est en liste d'attente.
La suppression d'un de ces nœuds inutiles s'effectue lors de son traitement. Nous comptons ses fils réellement placés dans l'arbre de recherche. Si aucun fils n'est gardé à la fin de son traitement, nous décidons de supprimer le nœud de l'arbre.
Sur base de nombreuses exécutions de notre solveur, nous avons remarqué que cette méthode nous permettait d'économiser en moyenne 30% de la structure de l'arbre de recherche. Ce résultat a pu être obtenu en comparant le nombre de nœuds traités et le nombre de nœuds réellement stockés dans l'arbre de recherche. Ce pourcentage ne nous parait pas incroyable. De fait, nous avons vu que, dans un arbre binaire complet, les feuilles représentent environ la moitié de la structure de l'arbre. Notre arbre de recherche n'est pas binaire et encore moins équilibré mais un gain non négligeable est quand même présent.
Nous avons voulu pousser l'idée jusqu'à supprimer des sous-arbres complets de l'arbre de recherche qui ne pourraient plus s'étendre. L'objectif était de remonter dans l'arbre de recherche lorsqu'une feuille était trouvée et de supprimer le plus haut nœud pour lequel tous les descendants étaient inutiles. L'idée fonctionnait très bien sur certains niveaux mais, étant donné qu'un nœud peut parfois être obtenu via plusieurs chemins différents, il arrivait que la méthode boucle en repassant de très nombreuses fois sur des chemins qui étaient chaque fois supprimés.
Cette technique n'est efficace qu'avec une bonne organisation des nœuds en attente. En effet, si nous parcourons en priorité les nœuds pour lesquels est petit, nous obtenons un parcours proche du parcours en largeur. Le résultat est que les feuilles mortes apparaîtront souvent très tardivement dans la recherche ce qui en réduit l'intérêt. Plus le parcours de l'arbre de recherche ressemble à un parcours en profondeur, plus la méthode est efficace. Les tris de liste d'attente conseillés dans les parcours A* et IDA* (cf. Sections 6.4.3 et 6.5.5) sont adaptés à un bon fonctionnement de l'élagage de l'arbre de recherche.
Chapitre 13 Résultats
Ce chapitre présente les résultats de l'exécution de notre solveur bestPushes sur les 90 niveaux originaux de Sokoban. Ceux-ci constituent une bonne base de tests commune à la plupart des solveurs existants.
13.1 Généralités
Dans ce mémoire, nous avons présenté un nombre conséquent de méthodes diverses et complémentaires. Tester chaque combinaison de ces méthodes sur les 90 niveaux se serait avéré long et fastidieux. Il faut en effet compter plusieurs heures pour un bon pré-traitement ainsi que plusieurs heures pour la résolution en elle-même. C'est pourquoi nous n'indiquons que les derniers résultats qui ont été obtenus avec l'utilisation de toutes les méthodes présentées.
Pour plus d'information sur les répercussions de chaque méthode sur le parcours effectué ainsi que sur la taille de l'arbre, il est conseillé de se référer àJunghanns (1999) qui comprend de nombreux tests à ce sujet.
-
La détection des doublons à l'aide de la table de hachage. Elle permet d'éviter les sous-arbres identiques et les cycles dans l'arbre.
-
Les parcours A* et IDA* qui améliorent grandement l'efficacité du parcours de l'arbre par rapport aux parcours en largeur et en profondeur. L'utilisation des méthodes les plus performantes pour calculer influe beaucoup sur la taille de l'arbre.
-
Les différentes méthodes de deadlock qui réduisent considérablement la taille de l'arbre de recherche.
-
La recherche passive et active de sous-états pénalisés pour affiner la valeur de .
Chaque amélioration citée permet d'utiliser de moins en moins de nœuds pour trouver la solution optimale d'un niveau.
-
4000000 nœuds à l'aide du parcours en largeur et de la méthode des doublons.
-
600000 nœuds avec le parcours IDA* et les deadlocks simples.
-
200000 nœuds avec la recherche passive de deadlocks de 3 caisses.
-
1500 nœuds avec la recherche passive de pénalités de 3 caisses.
-
106 nœuds avec la recherche active de pénalités et l'utilisation des macro-poussées.
Toutes les méthodes sont complémentaires les unes des autres. Si l'une d'entre elles n'est pas activée, les résultats se montreront nettement moins bons.
13.2 Tableau des résultats
-
Le nombre de poussées de la meilleure solution existante provient deOriginalHighScore (Pas d'année) etExtraHighScore (Pas d'année). Son optimalité n'est pas garantie mais elle a de grandes chances de l'être.
-
Le pré-processing représente le nombre de caisses utilisées lors de la recherche des sous-états pénalisés. Si le chiffre est 3, cela signifie que tous les sous-états pénalisés de 3 caisses et moins ont été trouvés avant de résoudre le niveau.
-
L'itération IDA* en cours () contient la dernière itération du parcours IDA* atteinte par le solveur.
-
Le nombre de poussées/mouvements de la solution trouvée. Les solveurs bestPushes et Rolling Stone trouvent la solution optimale. Le solveur Talking Stone (2) créé par Jean-Noël Demaret trouve une bonne solution qui sera rarement optimale.
-
Les nœuds explorés correspondent aux nombres de nœuds de l'arbre de recherche qui ont été explorés, lors de la dernière itération d'IDA*, avant de trouver une solution.
Le parcours lent
C'est le parcours qui est le plus puissant. Une recherche active de pénalités sera appliquée sur la dernière caisse poussée de chaque état rencontré dans l'arbre de recherche. Le but étant de pouvoir détecter un maximum de sous-états pénalisés. L'arbre de recherche s'en trouvera fort réduit mais, en contrepartie, le parcours sera très lent.
Le parcours rapide
C'est un parcours qui est moins puissant mais qui avance plus vite. Une recherche active ne sera appliquée que tous les 100000 états rencontrés dans l'arbre de recherche. Celle-ci s'appliquera sur toutes les caisses de l'état. Cette précaution doit permettre de détecter les plus grosses pénalités à moindre coût.
Il est aussi possible d'utiliser un parcours lent pendant quelques milliers de nœuds pour détecter le plus de sous-états pénalisés possibles pour ensuite utiliser un parcours rapide qui bénéficiera de ceux-ci.
Chapitre 14 Perspectives
Ce chapitre contient quelques pistes pour une future évolution du solveur. Certaines concernent des améliorations de méthodes déjà utilisées et d'autres proposent d'ajouter de nouvelles méthodes.
14.1 Pénalités probables : améliorations
La méthode de détection des pénalités probables en post-traitement est actuellement très naïve. Elle peut certainement s'avérer plus performante à l'aide des deux améliorations suivantes.
14.1.1 Détection d'ensembles de positions occupées simultanément
Nous avons parlé du post-traitement dans le Chapitre 11. L'une des méthodes proposée consistait à analyser l'arbre de recherche après l'exécution du solveur pour en déduire les sous-états dont la probabilité d'être pénalisés était forte.
Notre méthode était de trouver les positions les plus souvent occupées par des caisses pour en déduire une longue liste de sous-états à tester. Une meilleure approche consisterait à détecter non pas les positions les plus utilisées mais les ensembles de positions les plus utilisées simultanément. Bien entendu, un travail bien plus important sur l'arbre de recherche devra être effectué.
L'avantage d'une telle approche est que les ensembles de positions les plus souvent présents dans l'arbre de recherche vont souvent correspondre à une nouvelle pénalité. Dans le cas actuel où on crèe tous les sous-états possibles à partir de 15 positions différentes, on utilise plutôt une méthode de type brute force qui indiquera un taux bien plus bas de sous-états pénalisés.
14.1.2 Détection dynamique des pénalités probables
Le post-traitement consiste à attendre qu'un parcours se termine infructueusement sur un arbre de recherche pour pouvoir analyser ce dernier. Il pourrait être envisageable de ne pas attendre la fin du parcours pour effectuer cette analyse.
Le but premier de la méthode serait de détecter qu'un sous-ensemble de caisses reste constant dans l'un des sous-arbres de l'arbre de recherche, signe d'une pénalité non détectée. Une technique envisagée serait d'associer un compteur à chaque nœud qui indiquerait le nombre total de ses descendants. À chaque ajout d'un nœud dans l'arbre, le compteur de tous ses parents serait incrémenté.
Lorsqu'un nœud dépasserait un certain nombre de descendants, l'analyse du sous-arbre formé par ce nœud serait effectuée dans le but de trouver des caisses qui ne bougent pas. Un test classique de pénalité sera alors appliqué sur le sous-état formé par ces caisses.
14.2 Pénalités restrictives
Sur base de nos résultats et de ceux du solveur Rolling Stone, on remarque que certains niveaux sont difficiles à résoudre
1
. Ceux-ci correspondent généralement aux niveaux dont les aires des goals sont multiples (cf. Figure 14.1) ou pour lesquels plusieurs entrées sont possibles pour une unique aire de goal (cf. Figure 14.2). Par aire de goals, nous parlons d'un ensemble de positions voisines qui sont des goals. En effet les goals sont souvent proches les uns des autres.
Une raison pour laquelle ces niveaux sont plus difficiles est qu'il arrive souvent que la pénalité d'un sous-état n'affecte qu'un certain sous-ensemble de goals (cf. Figure 9.5). Nous appellerons ces pénalités particulières des pénalités restrictives. Selon les méthodes utilisées, ces pénalités ne peuvent pas être gardées. Le but de la validation de pénalité est justement de ne garder que celles qui s'appliquent indépendamment de la destination des caisses.
Si ces pénalités pouvaient être prises en compte lors du parcours de l'arbre, il est évident que les coûts des nœuds seraient plus précis et par conséquent que la recherche de solution serait plus efficace.
Le problème est que ces pénalités restrictives sont assez difficiles à utiliser pour les raisons suivantes :
-
Détection Pour être sûr de pouvoir détecter toutes les pénalités restrictives, il faudrait tester la pénalité de chaque sous-état de caisses vers tous les sous-ensembles possibles de goals. Un traîtement qui sera très coûteux s'il est fait systématiquement.
-
Stockage S'il faut stocker chaque sous-état relativement à des goals particuliers, le nombre d'informations en mémoire risque d'exploser et la recherche de la pénalité va s'avérer fastidieuse.
-
Application Actuellement, si un sous-état pénalisé est compris dans l'état en cours, la pénalité trouvée sera ajoutée à l'estimation de l'état. Pour appliquer une pénalité restrictive, il faudrait adapter la méthode hongroise de la Section 7.2.3 pour minimiser l'association caisses-goals en prenant en compte cette pénalité.
Si une méthode est trouvée pour résoudre le problème des pénalités restrictives tout en contournant ces trois difficultés, nul doute qu'elle symbolisera une nouvelle avancée dans la résolution de niveaux de Sokoban.
14.3 Macro-Tunnels
La méthode des Macro-Tunnels provient deJunghanns (1999) et consiste à détecter des tunnels dans les niveaux. Un tunnel est une succession de positions qui forment une ligne bornée sur deux côtés par des murs tel qu'illustré sur la Figure 14.3. Si deux caisses s'engagent en même temps dans un tunnel, elles y resteront bloquées et formeront un deadlock.
La technique utilisée dans les macro-tunnels consiste à téléporter une caisse qui rentre dans un tunnel directement vers sa sortie (de E6 à H6 et vice-versa). Le nombre moindre de positions pouvant être occupées par des caisses mènera à un arbre de recherche plus petit.
Dans les faits, la technique des macro-tunnels ne permet pas d'améliorer les performances du solveur de façon surprenante, mais le faible coût lié à son implémentation suffit à justifier sa présence.
Chapitre 15 Conclusion
Le but de ce mémoire était de créer un programme qui permettait de rechercher et de trouver les solutions optimales de niveaux de Sokoban. Grâce à l'implémentation de nombreuses méthodes provenant de précédentes recherches et à l'intégration de nouvelles fonctionnalités, nous pouvons dire que cet objectif est atteint. À ce jour, notre solveur a réussi à trouver 20 solutions optimales à partir des 90 niveaux originaux que nous avons testés.
L'implémentation en C++ d'un ensemble de méthodes existantes concernant le parcours, les deadlocks ou les pénalités a été l'un des gros enjeux de ce mémoire. Il a en plus été possible d'intégrer des nouvelles méthodes personnelles à celles existantes. Les nouvelles fonctionnalités les plus pertinentes concernent les deadlock zones, les deadlocks en Z, l'amélioration de l'estimation d'un niveau à l'aide d'un graphe connexe sophistiqué et, d'une manière plus générale, le concept des zones et des traitements binaires.
Après autant de travail, il peut paraître déconcertant de n'obtenir qu'une vingtaine de solutions optimales. Ce faible taux de résultats est en partie dû à un manque de temps de calcul. En effet, entre la dernière version stable du solveur et la date de remise du mémoire, il n'y a eu que quelques semaines. Celles-ci ont dû être mises à profit pour pré-traîter au mieux les niveaux et essayer de les résoudre. Le pré-traitement a occupé une grande partie de ce temps n'en laissant que peu pour la résolution. Nul doute qu'avec plus de temps, d'autres résultats auraient pu être obtenus. De fait, alors que certains niveaux n'ont été testés que quelques minutes, ceux pour lesquels la recherche a été la plus poussée n'ont pas été testés au delà de quelques centaines de milliers de nœuds : ce qui équivaut à moins de 100Mo de ram. Une marge de progression est donc possible.
Il peut être intéressant de considérer l'ensemble des sous-états pénalisés trouvés pour chaque niveau comme des résultats intermédiaires de ce mémoire. En effet, ce sont des résultats utiles qui pourraient éventuellement être réutilisés par d'autres solveurs.
Il y a un point pour lequel notre solveur n'a pas à rougir : le nombre de nœuds parcourus lorsqu'une solution est trouvée. Dans notre tableau de résultats, il est en effet très fréquent que notre arbre de recherche contienne moins de nœuds que celui de Rolling Stone lorsqu'une solution est trouvée. Cette différence provient sûrement de notre méthode des macro-poussées qui privilégie les poussées vers les positions les plus intéressantes.
Les évolutions de notre solveur sont possibles dans deux directions différentes. La première consiste à ajouter et améliorer les méthodes qui conservent l'optimalité des solutions. La deuxième consiste à ajouter des heuristiques très puissantes, telles que celles présentées par Jean-Noël Demaret dans Talking Stone (2)Demaret (2007), sur chaque état exploré de notre arbre de recherche. En ajoutant de bonnes heuristiques à l'efficacité du parcours décrit dans ce mémoire, il est fort probable que le nombre de solutions non-optimales trouvées soit assez important.
Lors de la rédaction de ce mémoire, l'accent a été mis sur la description des méthodes à l'aide d'exemples illustrés et en évitant d'insérer trop de pseudo-code pour ne pas alourdir la lecture. Pour plus de détails quant à l'implémentation de certaines méthodes, je vous suggère de vous référer au code et aux nombreuses pages de documentation générées à partir de celui-ci. Ces documents se trouvent sur le support numérique accompagnant ce mémoire ainsi que sur http://www.opengl.fr/memoire/.